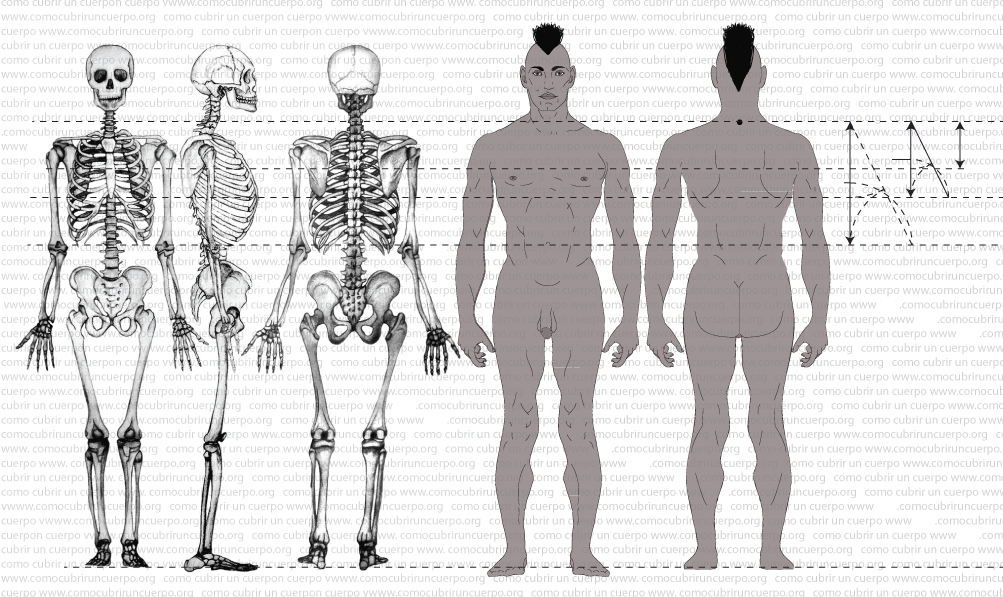
Medidas verticales a partir de la estatura

Previos: la proporción áurea y Erns Neufert

En este post examinaremos las proporciones áureas  del cuerpo humano propuestas por Erns Neufert (1900-1986) del que ya hablamos en post anteriores.

En esta ocasión vamos a desglosar las proporciones áureas que encontramos en el cuerpo humano de forma que podamos usarlas para poder deducir las medidas verticales.

Este estudio se basará en la estatura y en la primera parte de este post reduciremos la estatura total de la persona a la altura de séptima vertical hasta suelo, luego buscaremos la altura de la entrepierna para así poder centrarnos en el torso (desde la séptima cervical hasta la próstata)

Luego hallaremos la cintura y la línea de sisa.

Evidentemente no debemos tomar estas medidas al pie de la letra pero pueden ser muy útiles para poder deducir medidas que no podemos encontrar en las tablas.

Cabe recordar aún una vez más que el hombre perfecto no existe y que cada cuerpo es un mundo, pero dado en que vivimos en una era en que la costura a medida no da lugar, debemos encontrar una serie de prototipos proporcionales que sirvan para los cuerpos de una mayoría.

Al final del post incluimos una lista con los resultados de todas las operaciones que deducimos, algunas son secundarias, otras no y nos pueden facilitar mucho nuestra labor.

No os asustéis por las fórmulas, en verdad son simples, parecen muy complicadas por los paréntesis pero es la única forma en que podemos escribirlas para que aparezcan en WordPress.

Si os fijáis en la tabla veréis como es mucho más simple de lo que parece.

El número φ (phi)

Citando Wikipedia nos define el número Phi como:

El número áureo o de oro (también llamado razón extrema y media,razón áurea, razón dorada, media áurea, proporción áurea y divina proporción representado por la letra griega φ (phi) (en minúscula) o Φ (Phi) (en mayúscula), en honor al escultor griego Fidias, es un número irracional.

Se trata de un número algebraico irracional (su representación decimal no tiene período) que posee muchas propiedades interesantes y que fue descubierto en la antigüedad, no como una expresión aritmética sino como relación o proporción entre dos segmentos de una recta; o sea, una construcción geométrica. Esta proporción se encuentra tanto en algunas figuras geométricas como en la naturaleza: en las nervaduras de las hojas de algunos árboles, en el grosor de las ramas, en el caparazón de un caracol, en los flósculos de los girasoles, etc.

Asimismo, se atribuye un carácter estético a los objetos cuyas medidas guardan la proporción áurea. Algunos incluso creen que posee una importancia mística. A lo largo de la historia, se ha atribuido su inclusión en el diseño de diversas obras de arquitectura y otras artes, aunque algunos de estos casos han sido cuestionados por los estudiosos de las matemáticas y el arte.

^]Recordemos antes de empezar que el número φ es igual a 1.61803398874989…, nosotros consideraremos sólo los tres primero s decimales: 1.618.

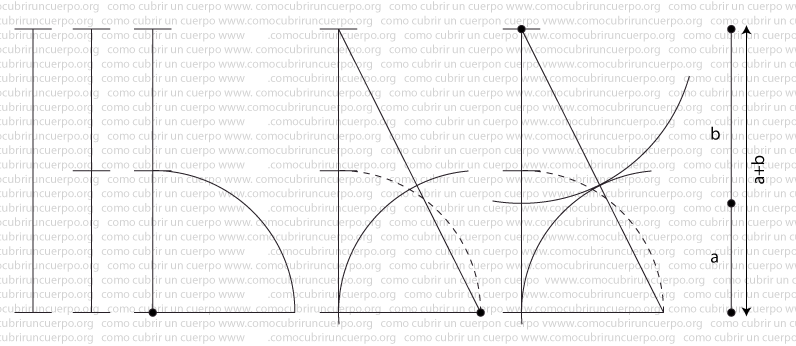
Podemos trazar directamente el número φ sin necesidad de calcularlo, en la siguiente ilustración mostramos cómo hacerlo:

En la parte más a la izquierda de la ilustración mostramos un segmento. En esta ilustración mostraremos como dividir este segmento en dos que mantengan entre ellos  la proporción áurea.

Para empezar dividiremos el segmento en dos partes iguales (segunda imagen de la siguiente ilustración) y desde una de las bases del segmento trazaremos un arco cuyo radio sea igual a la mitad del recorrido del segmento trazaremos una perpendicular al segmento original hasta que cruce con el arco (tercera imagen de la siguiente ilustración).

Uniremos el punto en que se cruza el arco con la perpendicular hecha al segmento original con el punto del segmento opuesto al que hemos utilizado como centro del arco (cuarta imagen de la siguiente ilustración). Desde el punto en que se cruza el arco con el segmento original trazaremos un arco cuyo recorrido sea igual al recorrido de la perpendicular hasta que corte la línea inclinada.

Desde el punto en que se cruza la línea inclinada con el segmento original trazaremos un arco cuyo radio sea igual a la distancia entre su centro y el punto en que se cruza el segundo arco trazado sobre la línea diagonal. El punto en que se cruza este último arco con el segmento original será el punto que dividirá el segmento original en dos (a y b) que mantendrán entre ellos la proporción áurea.

Deducción de las medidas verticales a través del número φ

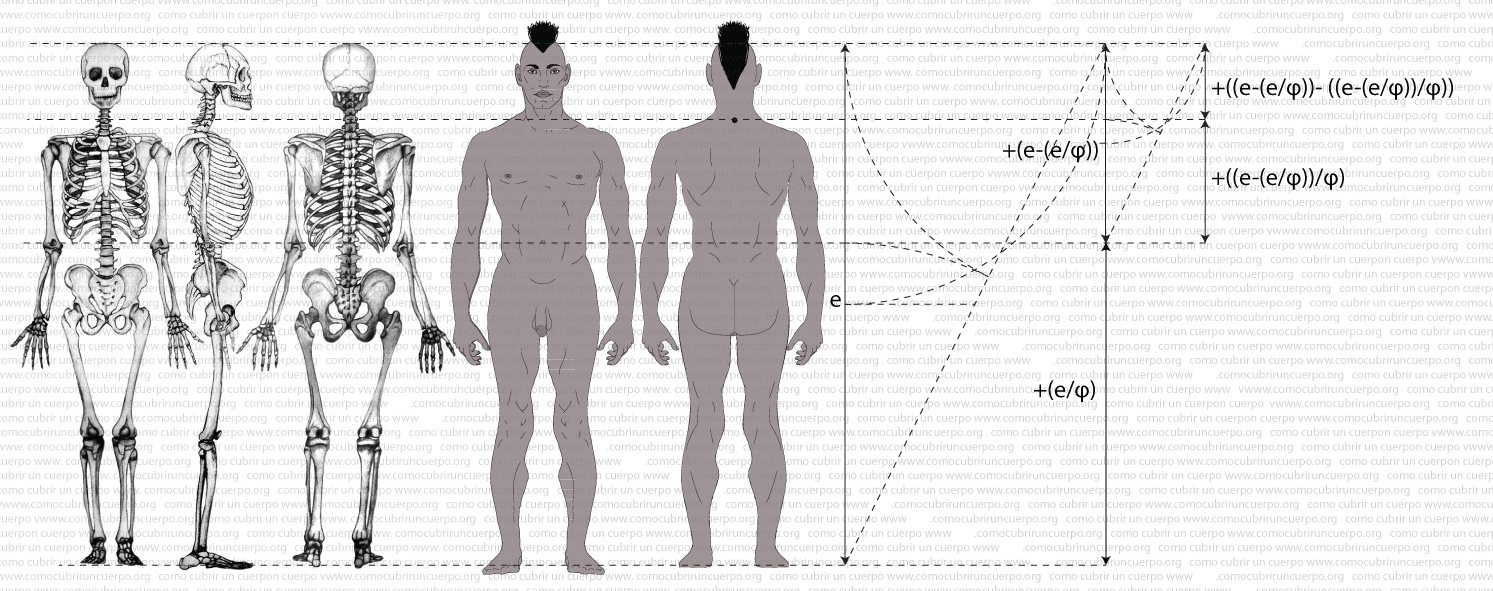
1.- Si dividimos la estatura (e) por el número φ  nos dará un valor: +(e/φ) obtendremos la medida de suelo a ombligo, que por la parte de la espalda coincide con la línea de riñones. Esta línea horizontal nos sirve para entallar las piezas de cintura: las levitas, los  fracs, spencers,  etc.

2.- Si restamos de la estatura la medida anterior obtendremos la medida desde la coronilla a ombligo: +(e-(e/φ)).

3.- Si dividimos por φ la medida anterior obtendremos la distancia entre el ombligo y séptima vértebra: +((e-(e/φ))/φ)

4.- Si restamos la medida ombligo coronilla de la distancia ombligo séptima vértebra obtendremos la medida séptima vértebra coronilla: +((e-(e/φ))- ((e-(e/φ))/φ))

5.- Si restamos la estatura de la medida anterior obtendremos la medida desde la séptima vertebra al suelo: +(e-((e-(e/φ))- ((e-(e/φ))/φ)))

6.- Si dividimos por φ la medida suelo ombligo obtendremos la medida de ombligo a rodilla: +((e/φ)/φ))

7.-Si restamos la medida que acabamos de obtener a la medida de suelo ombligo obtendremos la medida suelo- rodilla: +((e/φ) – ((e/φ)/φ)))

8.- Si dividimos la medida de ombligo a rodilla por el número φ obtendremos la medida de  desarrollo de muslo a ombligo: +(((e/φ)/φ))/φ)

9.- Si restamos la medida anterior de la medida de ombligo rodilla obtendremos el valor de rodilla a desarrollo de muslo: +(((e/φ)/φ))- (((e/φ)/φ))/φ))

10.- Si dividimos la medida de desarrollo de muslo a ombligo por el número φ, obtendremos el valor de ombligo a entrepierna: +((((e/φ)/φ))/φ)

11.- Si restamos el desarrollo de muslo a ombligo de la medida de ombligo a entrepierna encontraremos la medida de  desarrollo de muslo a entrepierna: +((((e/φ)/φ))/φ))- ((((e/φ)/φ))/φ)

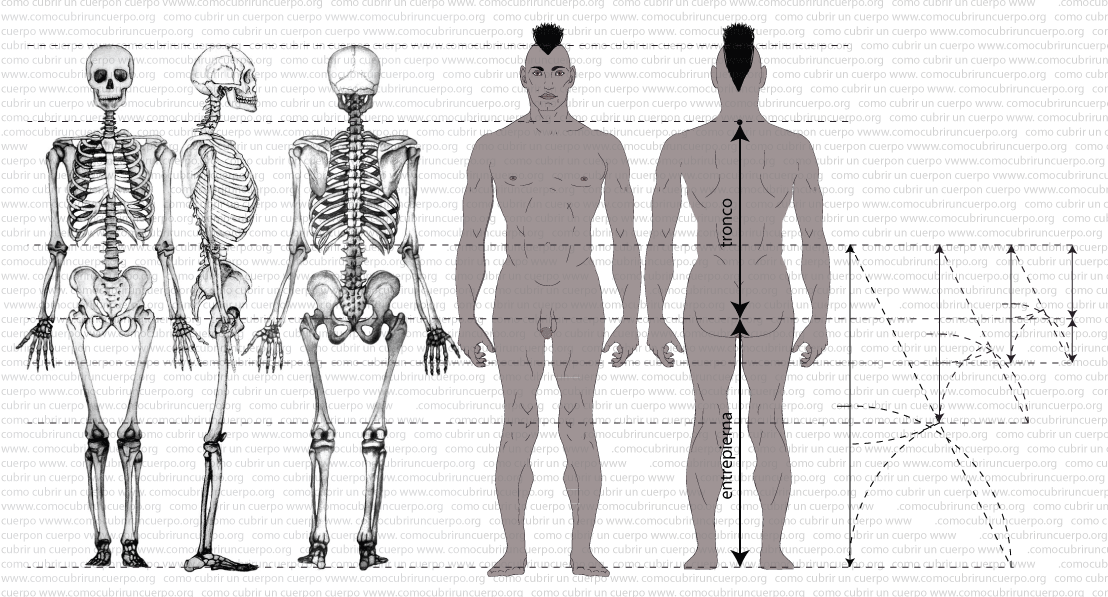
12.- Si sumamos el valor de ombligo a séptima cervical al valor de ombligo entrepierna obtendremos el valor de tronco: +(((e-(e/φ))/φ)+((((e/φ)/φ))/φ)/φ))

13.- Si sumamos el valor de suelo rodilla al de rodilla desarrollo de muslo y  el valor de desarrollo de muslo entrepierna hallaremos el valor entero de la entrepierna: +(((e/φ) – ((e/φ)/φ)))+(((e/φ)/φ))- (((e/φ)/φ))/φ))+ (((e/φ)/φ))-(((e/φ)/φ))/φ)))

En los 13 números anteriores hemos podido aislar el tronco de la estatura dividiendo el cierpo humano en tres partes: la cabeza (desde la coronilla hasta la séptima vertical), el tronco desde la séptima vertical hasta la próstata) y el entrepierna (desde la próstata hasta el suelo.

Ahora nos centraremos en el tronco.

14.- Si dividimos la medida de tronco por el número φ nos encontraremos el nivel desde la séptima vértebra hasta el punto más salido de la cresta ilíaca. Sabemos que la cresta ilíaca se alza de un centímetro y medio por encima de la línea de cintura. La línea de cintura la colocamos encima de los patrones al nivel de la medida del largo pierna detrás, que es un centímetro y medio más corto que el largo pierna lateral por ello esta medida la llamaremos séptima-cresta ilíaca: +((((e-(e/φ))/φ)+((((e/φ)/φ))/φ)/φ))/φ)

15.- Medida de Busto detrás: será la medida anterior más un centímetro y medio: +(((((e-(e/φ))/φ)+((((e/φ)/φ))/φ)/φ))/φ)+1.5)

16.- Si restamos de la medida de tronco  la medida de séptima-cresta ilíaca obtendremos la medida de entrepierna a cresta ilíaca:

+((((e-(e/φ))/φ)+((((e/φ)/φ))/φ)/φ))-((((e-(e/φ))/φ)+((((e/φ)/φ))/φ)/φ))/φ))

17.- Medida de montante de pantalón: será la medida anterior menos un centímetro y medio del alzamiento de la cresta ilíaca:

+(((((e-(e/φ))/φ)+((((e/φ)/φ))/φ)/φ))-((((e-(e/φ))/φ)+((((e/φ)/φ))/φ)/φ))/φ))-1.5)

 

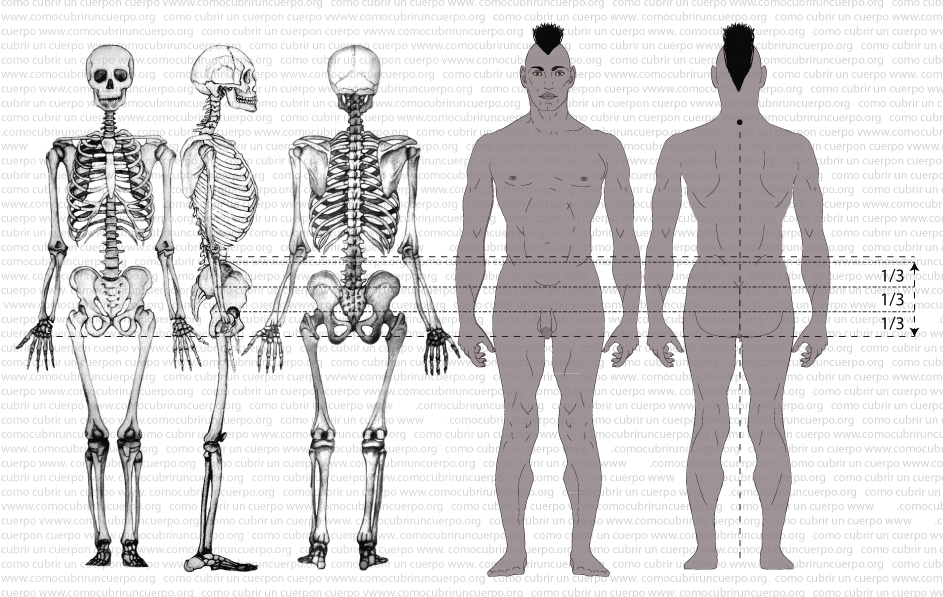
En la próxima ilustración mostramos el montante en tres tercios iguales que nos situarán el nivel de las “petites hanches” y de la cadera respectivamente desde la línea de cintura que se toma a partir de la medida de largo de pierna detrás.  (líneas discontinuas con los trazos más cortos)

18- Medida de altura de las “Petites Hanches”, se sitúa en el primer tercio del montante partiendo la línea de cintura hacia el entrepierna.

+(((((e-(e/φ))/φ)+((((e/φ)/φ))/φ)/φ))-((((e-(e/φ))/φ)+((((e/φ)/φ))/φ)/φ))/φ))+1,5)/3

19- Medida de altura de cadera, se sitúa a dos tercios del montante partiendo de la línea de cintura hacia el entrepierna:

+2(((((e-(e/φ))/φ)+((((e/φ)/φ))/φ)/φ))-((((e-(e/φ))/φ)+((((e/φ)/φ))/φ)/φ))/φ))+1,5)/3

Ahora nos concentraremos en la distancia entre el nivel del ombligo y el nivel de la séptima cervical.

20.- Si dividimos la distancia entre el ombligo y la séptima cervical por φ el resultado nos marcará la medida entre la séptima cervical  y la punta del apéndice xifoides del esternón:

+(((e-(e/φ))/φ)/φ)

21.- Si dividimos esta última medida (medida entre la séptima cervical  y la punta del apéndice xifoides del esternón) por el número φ nos dará la medida desde la séptima cervical hasta la altura de la línea de sisa:  +((((e-(e/φ))/φ)/φ)/ φ)

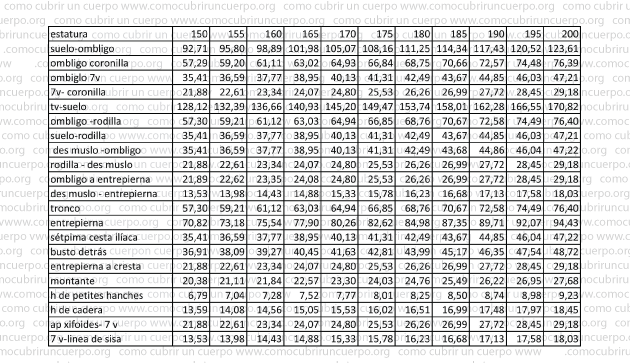
A continuación mostramos una tabla con todas las fórmulas que hemos utilizado en este post

En la tabla siguiente damos las medidas calculadas desde la estatura 150 hasta la de 200 cm.

Estas medidas están calculadas sobre un cánon, sobre una figura ideal.

Al utilizarlas debemos tener presente que son una indicación, siempre será mejor utilizar una serie de medidas de una tabla comprobada.

Repetimos otra vez aquí que las medidas estandarizadas no tienen porque corresponder a un cuerpo concreto, ya que las tablas de medidas se basan en unas proporciones o en una muestra de un grupo social, el cuerpo concreto que se viste puede o no responder a estas proporciones o estar fuera del grupo que hemos tomado como muestra.