El volante o volado de caracol
El volante o volado de caracol
El volante o volado de caracol se cortan mediante espirales.
Hay varios tipos de espirales
En costura nos interesarán las espirales de pasos conocidos y dentro de ellas las de dos, tres y cuatro centros.
Vayamos por pasos y guardemos la calma.
Una espiral es una curva abierta y plana generada por el movimiento de otro u otros fijos denominados centros.
En el caso que nos atañe estarán construidas por arcos de circunferencia enlazados entre sí y de radios gradualmente mayores.
Llamaremos espiral a la línea curva generada por un punto que se va alejando progresivamente del centro a la vez que gira alrededor de él
Llamaremos espira al fragmento de curva que describe el punto en una vuelta completa. Las espiras contiguas distan entre sí una magnitud constante llamada paso.
En este blog estudiaremos tres tipos de espirales, la de dos, tres y cuatro centros.
La de dos centros nos generará una espiral que tendrá un ancho constante entre las espiras, el de tres y cuatro centros nos generarán espirales en que el las espiras se distanciarán progresivamente.
La espiral de dos centros nos servirá para la mayoría de volantes, las otras dos para empezarlos y acabarlos cuando queramos que empiecen y acaben desde o hasta el ancho deseado.
Los de tres y cuatro centros nos pueden servir para patronar volantes que nazcan de cero y se conviertan en colas, por ejemplo en los trajes de novia.
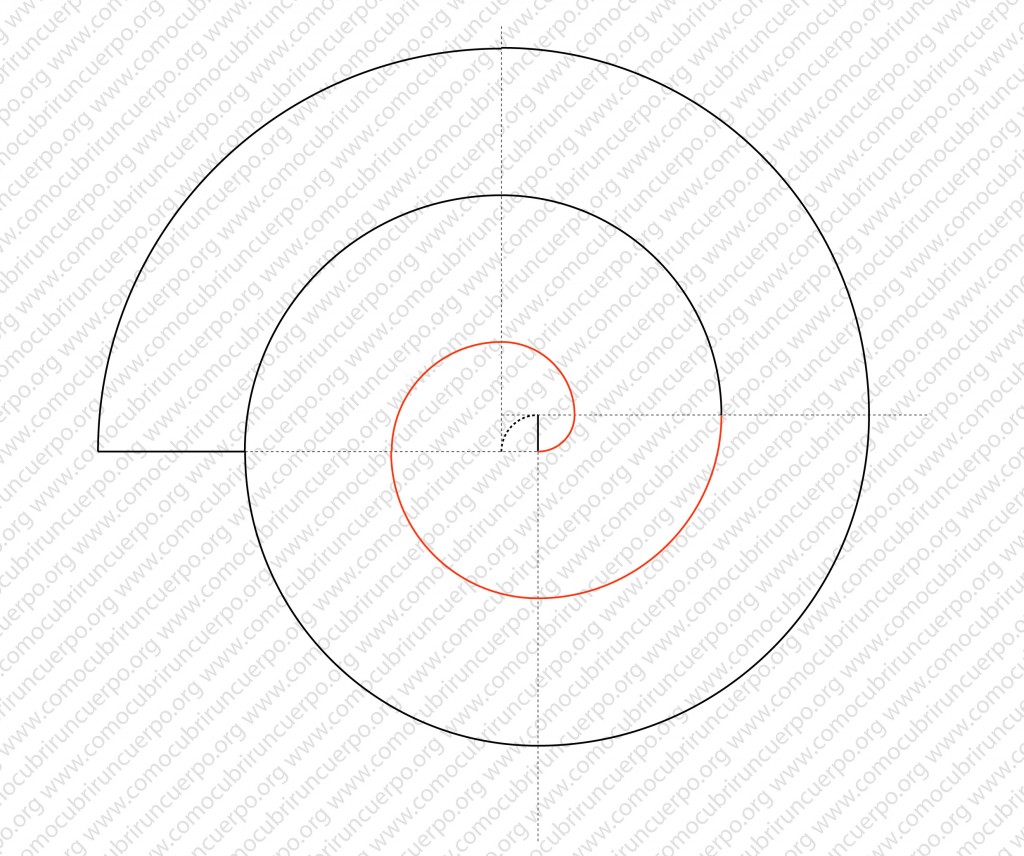
Forma de patronar volante de caracol que tenga siempre el mismo ancho: espiral de dos centros.
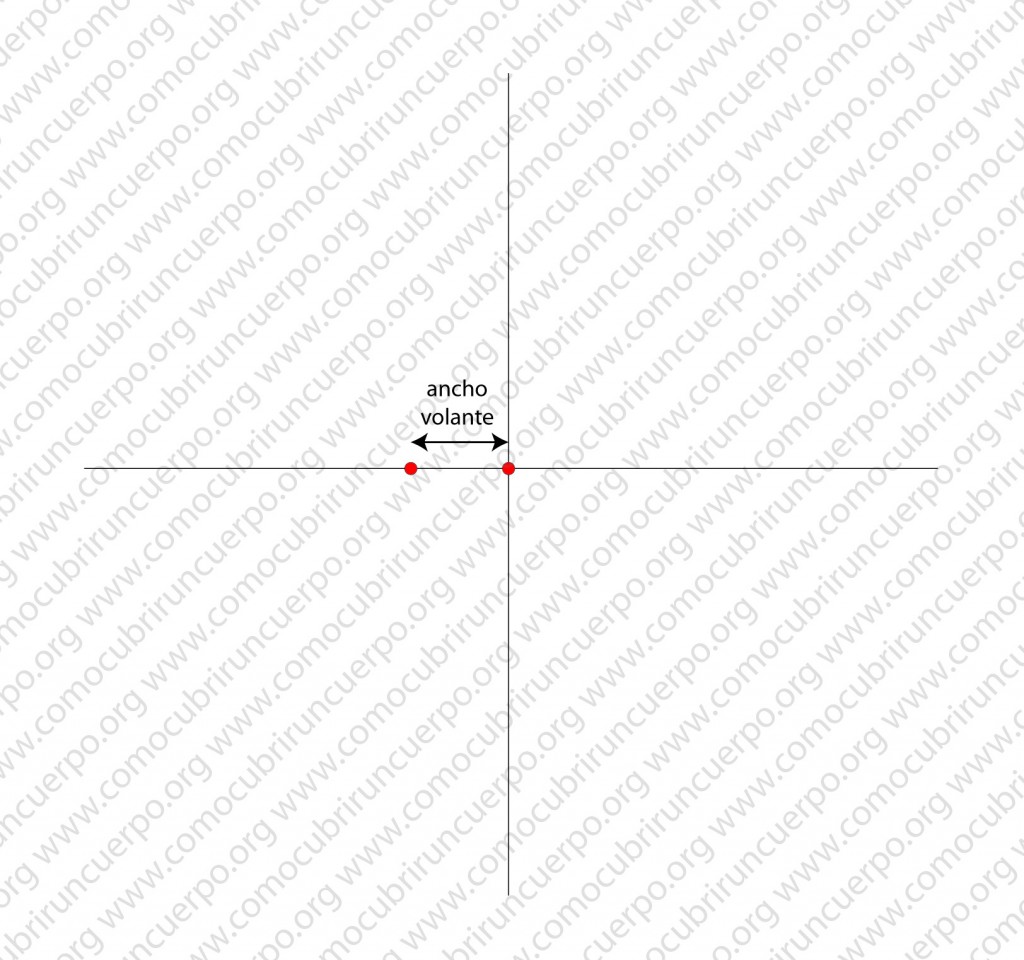
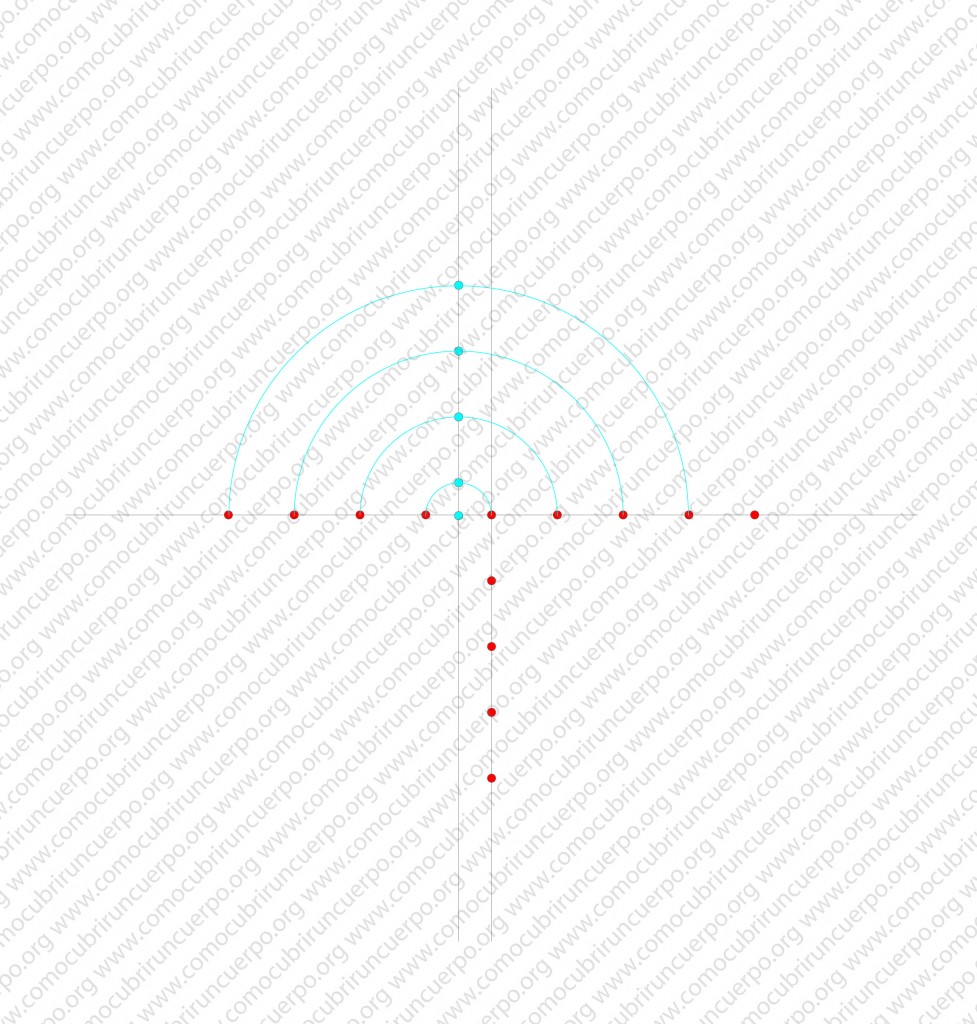
Trazaremos dos líneas perpendiculares.
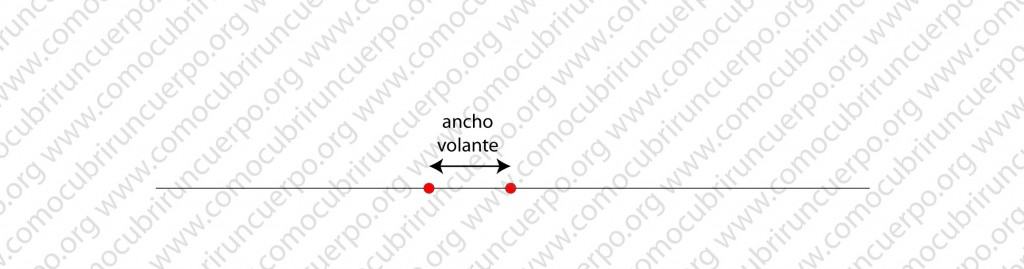
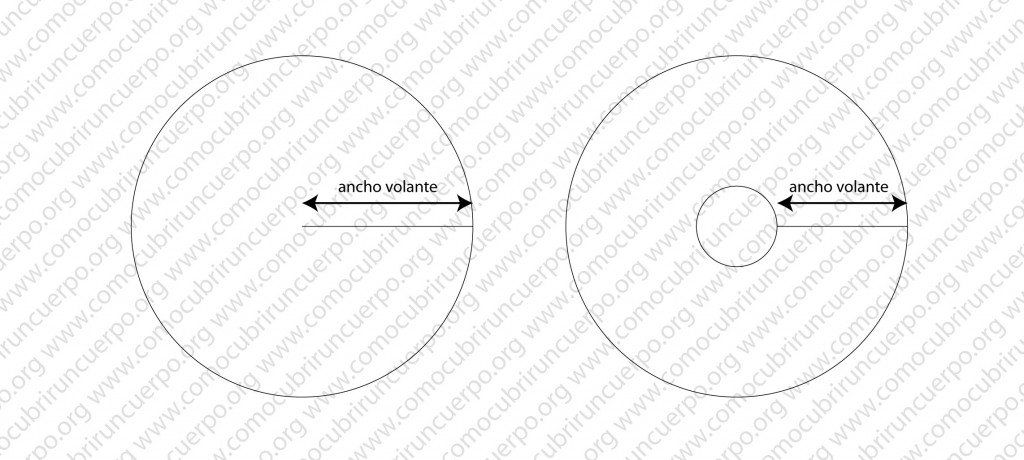
A partir del punto en que se cruzan anotaremos el ancho del volante deseado. El punto situado en la intersección de los dos ejes será el primer centro de la espiral. Puntos Rojos.
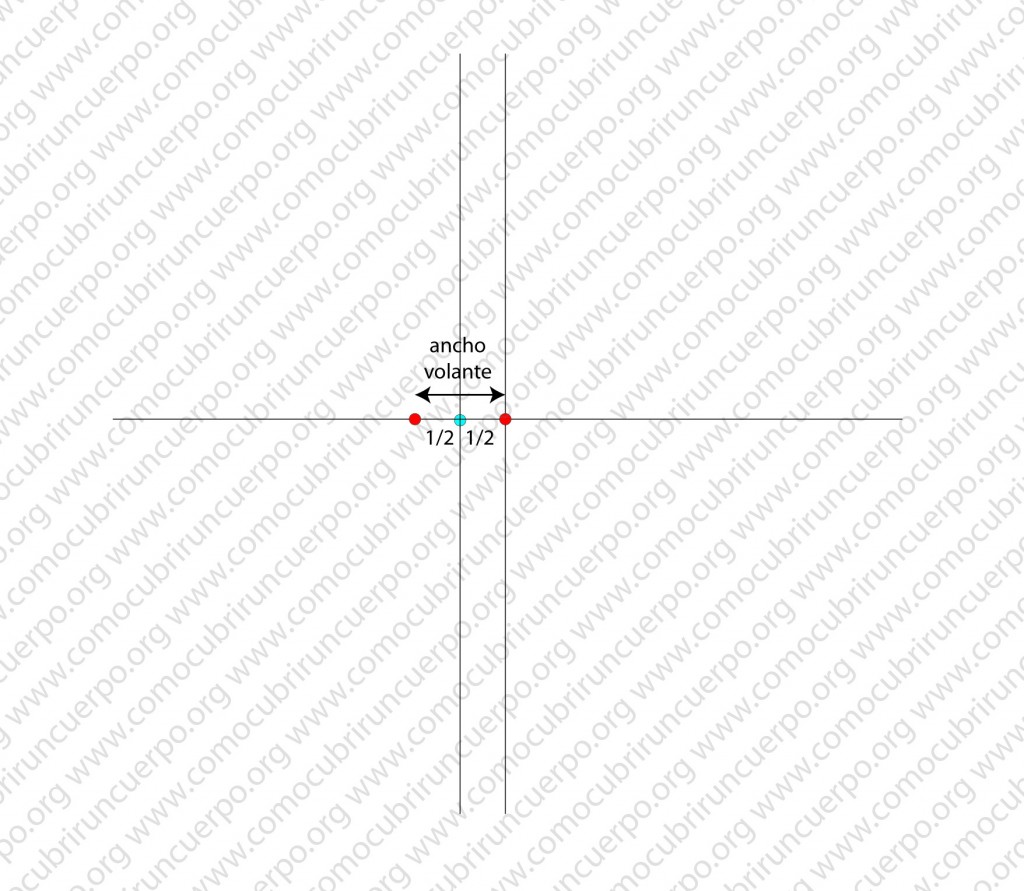
A mitad de distancia de los dos puntos anteriores anotaremos otro punto (azul). Este punto será el segundo centro. Sobre este punto trazaremos una perpendicular al eje de las x.
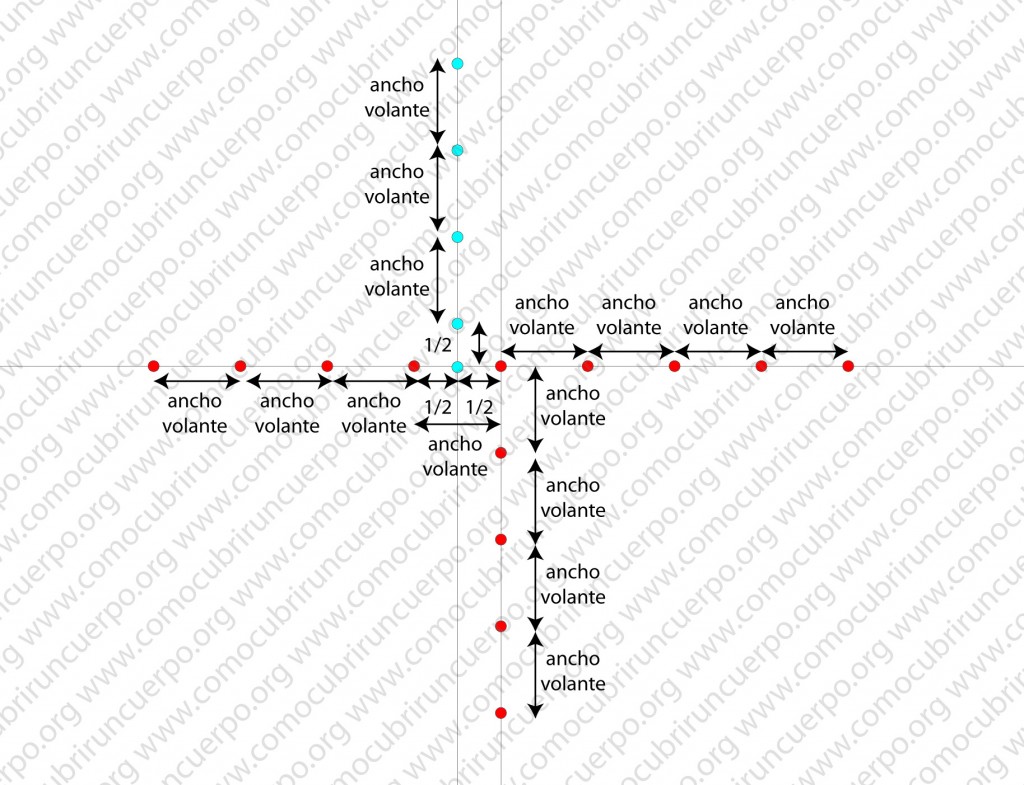
Sobre el eje de las x (línea horizontal) marcaremos sucesivamente de uno y otro lado de la intersección de los ejes, el ancho que queramos del volante hasta completar el área que deseamos emplear para éste (puntos rojos sobre la línea horizontal). Sobre la primera línea vertical que hemos realizado en el trazado anotaremos, en la parte inferior, el ancho del volante deseado (puntos rojos sobre la línea vertical.)
Sobre la paralela que hemos trazado a la primera línea vertical anotaremos en la parte superior de la línea, la mitad del ancho deseado para el volante y desde este punto anotaremos el ancho del volante deseado tantas veces como hayamos puesto a cada lado de la línea horizontal (puntos azules).
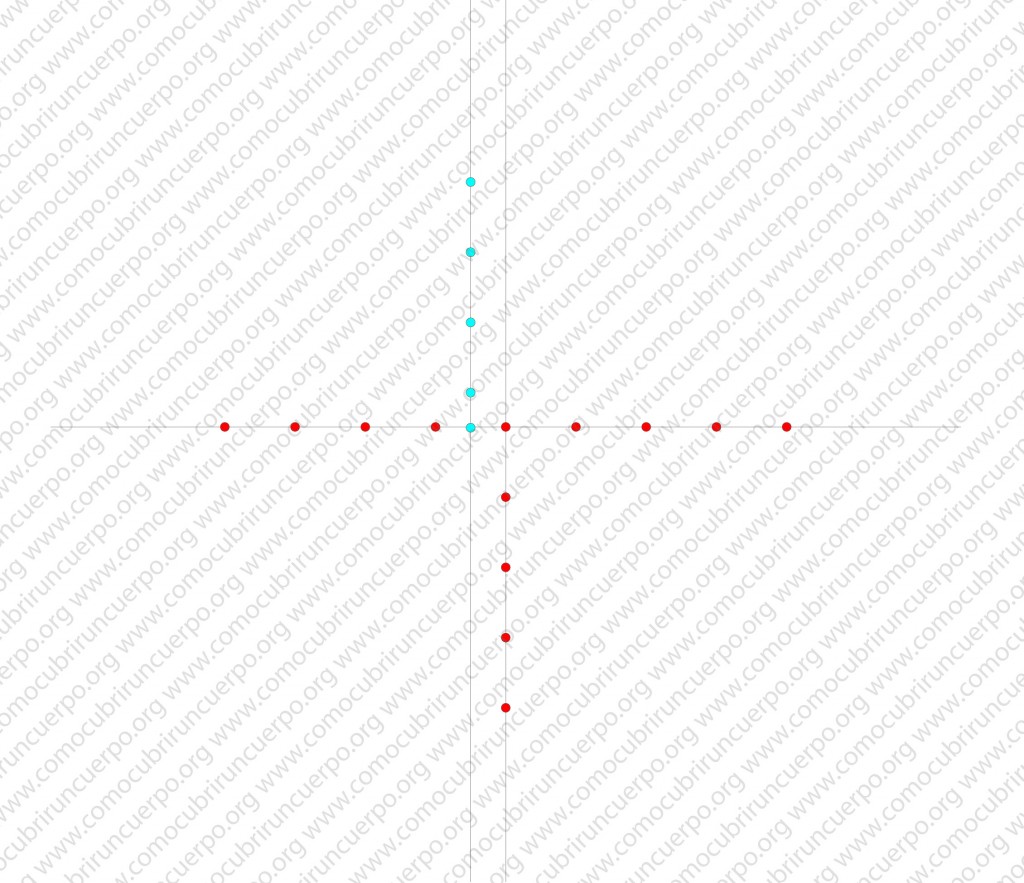
Los puntos trazados en las dos líneas verticales no son necesarios pero nos ayudan para establecer el espacio que ocupará el caracolillo. Borrando las acotaciones obtendremos el siguiente esquema:
Trazaremos encima de la línea horizontal a partir del segundo centro intersección de línea horizontal con segunda línea vertical (punto azul) una serie de semicircunferencias tal y como se muestra en la siguiente ilustración
Haremos lo mismo con el primer centro (el que corta las dos primeras líneas y que hemos marcado con un punto rojo).
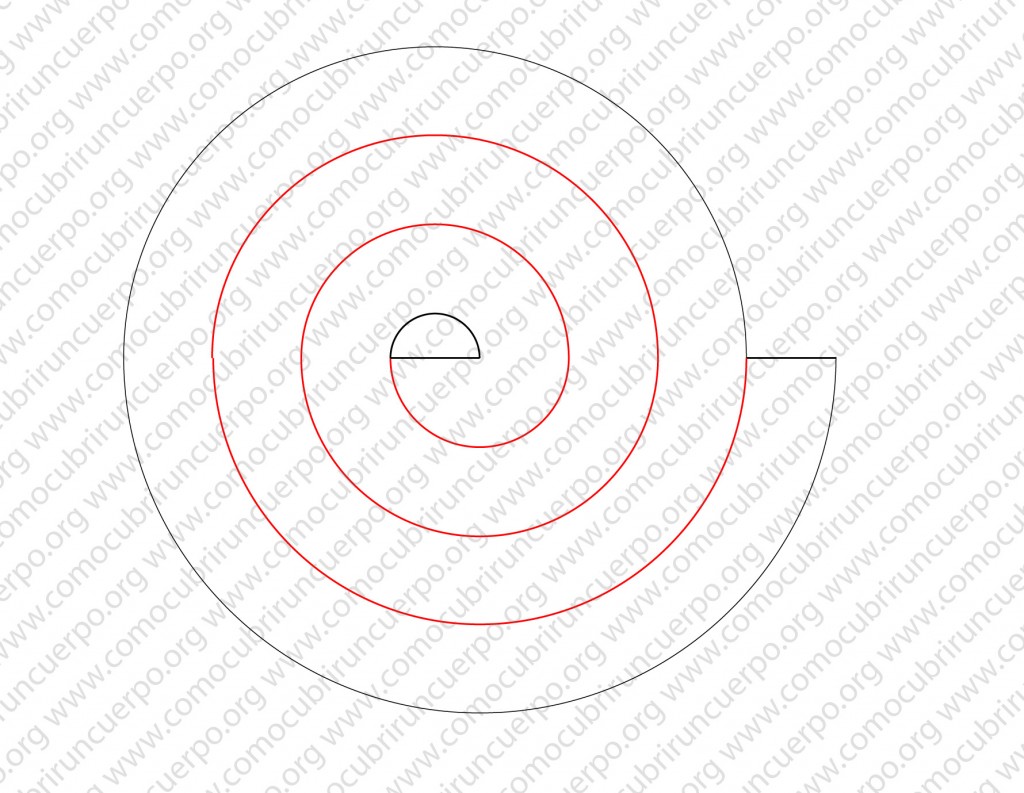
Nuestra espiral ya está acabada. Utilizaremos la línea horizontal para empezar y acabar el volante cortado en caracol.
La costura que ha generado este volante de caracol es la que marcamos en línea roja.
El vuelo de este volante (valga la redundancia), es el que hemos marcado con la línea azul.
Como podemos observar este volante tiene el mismo ancho desde el inicio hasta el final.
Forma de patronar un volante de caracol que crece: espiral de tres y cuatro centros.
Como comentábamos anteriormente, nos puede interesar un volante que crezca o que decrezca a medida que se desarrolla. Ello lo conseguiremos con el segundo y tercer tipo de espirales.
El segundo tipo de espirales son las de tienen un número de centros mayor a dos.
La espiral de tres centros está determinada por un triángulo, en nuestro caso, ya que queremos que su crecimiento sea constante, estará generado por un triángulo equilátero (de tres lados iguales)
Trazaremos una línea horizontal y marcaremos el ancho inicial que hemos decidido para el volante (que en su desarrollo se triplicará), como veremos más adelante.
Tazaremos dos arcos cuyos radios sean iguales a la distancia que separa los dos puntos. En la intersección de estos dos arcos marcaremos un tercer punto.
Uniremos los tres puntos encontrados y obtendremos nuestro triángulo equilátero (de tres lados iguales)
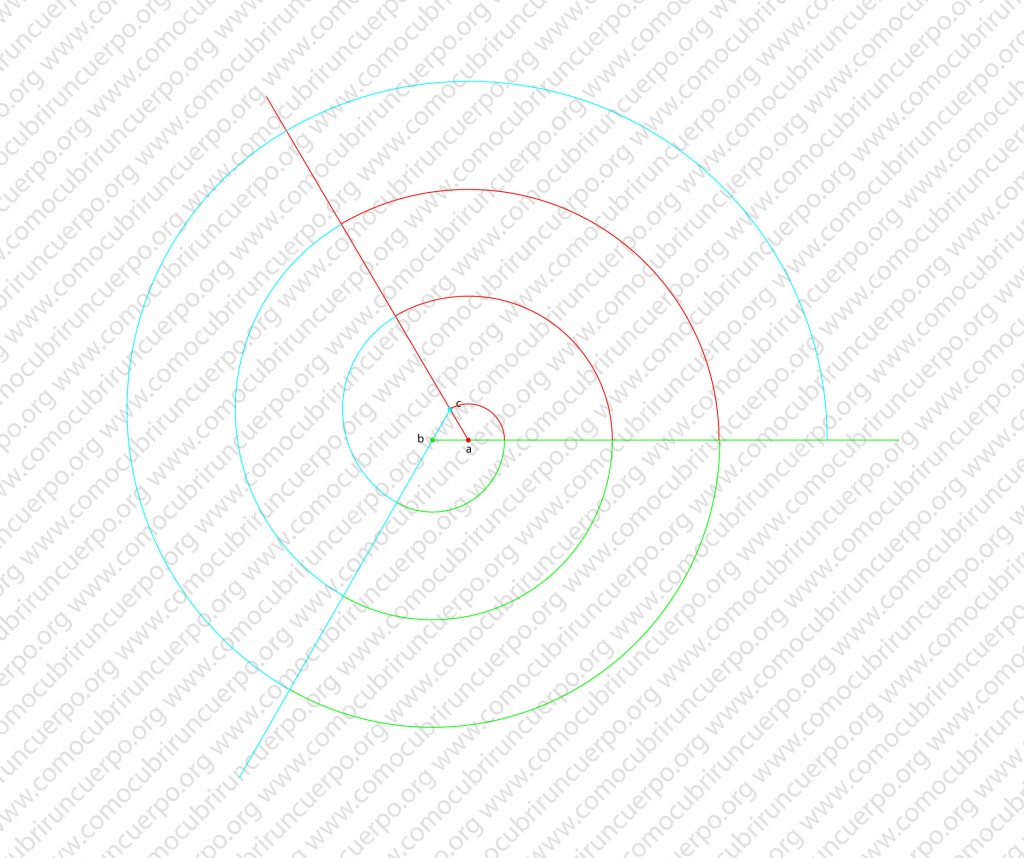
Prolongaremos en un mismo sentido los tres lados del triángulo y estableceremos como centro uno de los vértices, de esta forma obtendremos tres vértices. En la imagen: A (color rojo), B (color verde) y C (color azul).
Trazaremos la espiral. Empezaremos colocando el compás en el centro “a” con el radio igual a la distancia a-c y trazaremos desde el punto “c” un arco hasta cortar la línea de la prolongación de b (línea verde): el arco desde el punto a (rojo) desde C hasta la intersección de la línea B lo hemos marcado con un trazado continuo rojo ya que su centro “a” es de color rojo, seguiremos de la misma forma ahora punteando el compás desde el centro b (azul) y el radio la distancia entre el centro b y la intersección del arco anterior con la línea b , en la ilustración lo hemos marcado con una línea verde ya que el centro b es verde, este arco acabará en la intersección de la línea que contiene el punto c (color azul), pasaremos al centro c que es azul y procederemos de la misma forma.
Alternaremos los centros a, b, c, a, b, c,…..hasta conseguir el largo del volante deseado
Analizando esta espiral con la de dos centros vemos que no alcanza el ancho deseado del volante constante hasta el punto X, marcado con el punto naranja desde el inicio (punto azul hasta el punto naranja aumenta progresivamente cada vez que se corta con cada línea recta del valor del lado del triángulo equilátero, ello ocurre tres veces, por ello esta espiral tiene el paso tres (P/3).
La espiral generada por un triángulo, al tener tres centro, genera una espiral P/3 y ello quiere decir que durante los primeros 360 grados (una espira) crecerá desde un tercio del paso hasta estabilizarse en su ancho (P)
Para que el tercer sector de la primera vuelta tenga la forma redondeada trazaremos un tercio de circunferencia con el centro en el punto rojo, con un arco igual a un lado del triángulo desde el punto azul hasta el punto verde.
En el caso en que queramos que en la evolución de la primera vuelta la elipse cuadriplique el ancho del volante haremos una elipse de centros cuyo paso será P/4 y su figura base será un cuadrado.
Mostramos una elipse de cuatro centros en la ilustración siguiente.
De esta forma podemos determinar el comienzo de nuestro volante y el desarrollo en la primera vuelta.
Volante de caracol sobre el trazado de la espiral de Arquímedes.
Si lo que deseamos es un volante que nazca en un punto y de forma abrupta llegue a un ancho determinado, en 360 grados, lo mejor es trazar una espiral de Arquímedes.
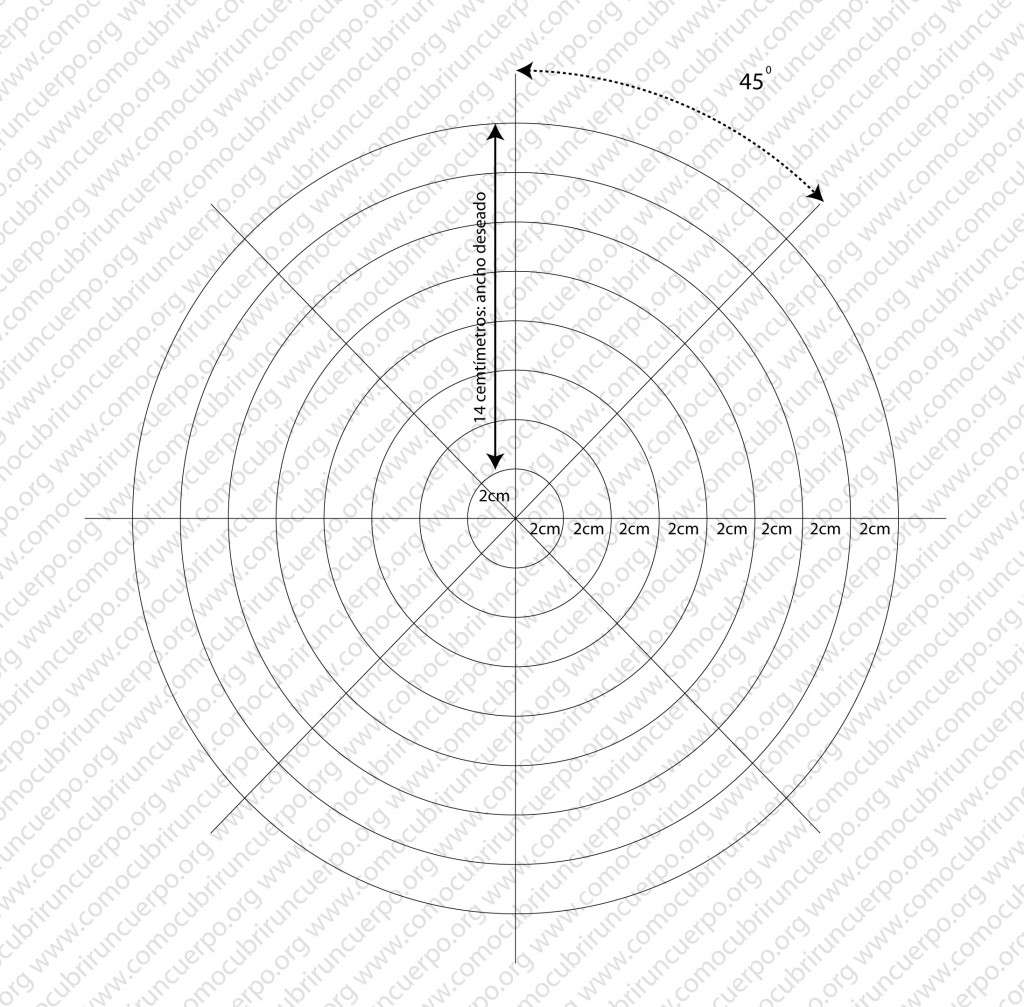
Imaginemos que queremos cortar un volante que vaya de 0 a 14 centímetros en 360 grados.
Buscaremos un múltiplo fácil para el ancho, en este caso 14 podemos descomponerlo en 2*7, dos es un número demasiado bajo por lo que tomaremos el número 7.
Trazaremos un par de líneas a escuadra y en su intersección, en sentido vertical, sobre el eje de las Y, pondremos el ancho más el ancho dividido por el número que hayamos elegido. O sea en nuestro caso 14+2= 16, luego trazaremos circunferencias concéntricas a partir de la intersección cuyo radio aumente del número que hemos sumado.
En nuestro caso circunferencias de 2, 4, 6, 8, 10, 12, 14, 16 y 18 cm de radio.
Luego dividiremos los grados de la circunferencia (360) entre el número elegido (7) más uno o sea 8; por lo que 360/8= 45 grados
Trazaremos radios a 45 grados hasta completar la circunferencia.
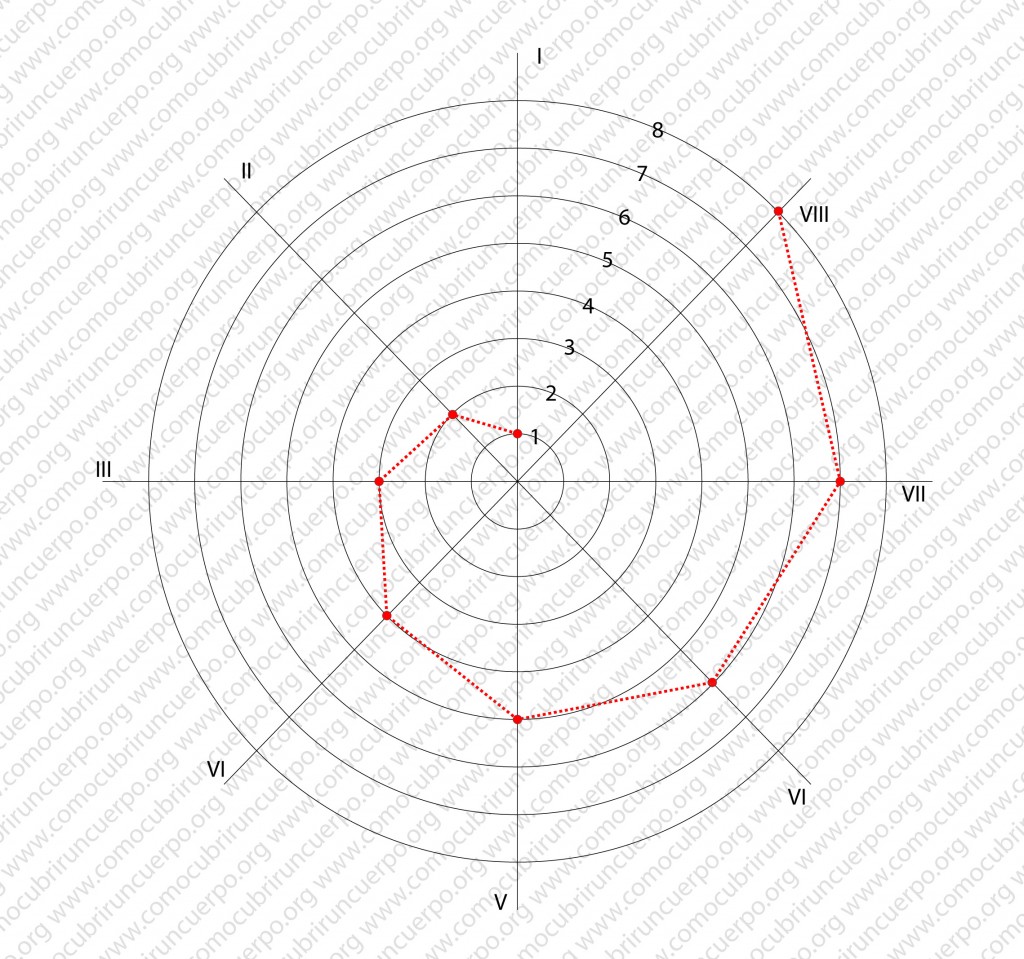
Numeraremos los radios en sentido anti horario (números romanos)
Numeraremos los círculos concéntricos del más pequeño hasta el mayor (números arábigos occidentales)
Uniremos las intersecciones I-1, II-2, III-3 y así sucesivamente hasta llegar al VIII-8 (representado en la ilustración con puntos rojos)
Uniremos los puntos de las intersecciones desde los más interiores hasta los más exteriores (indicado en la ilustración con una línea roja discontinua).
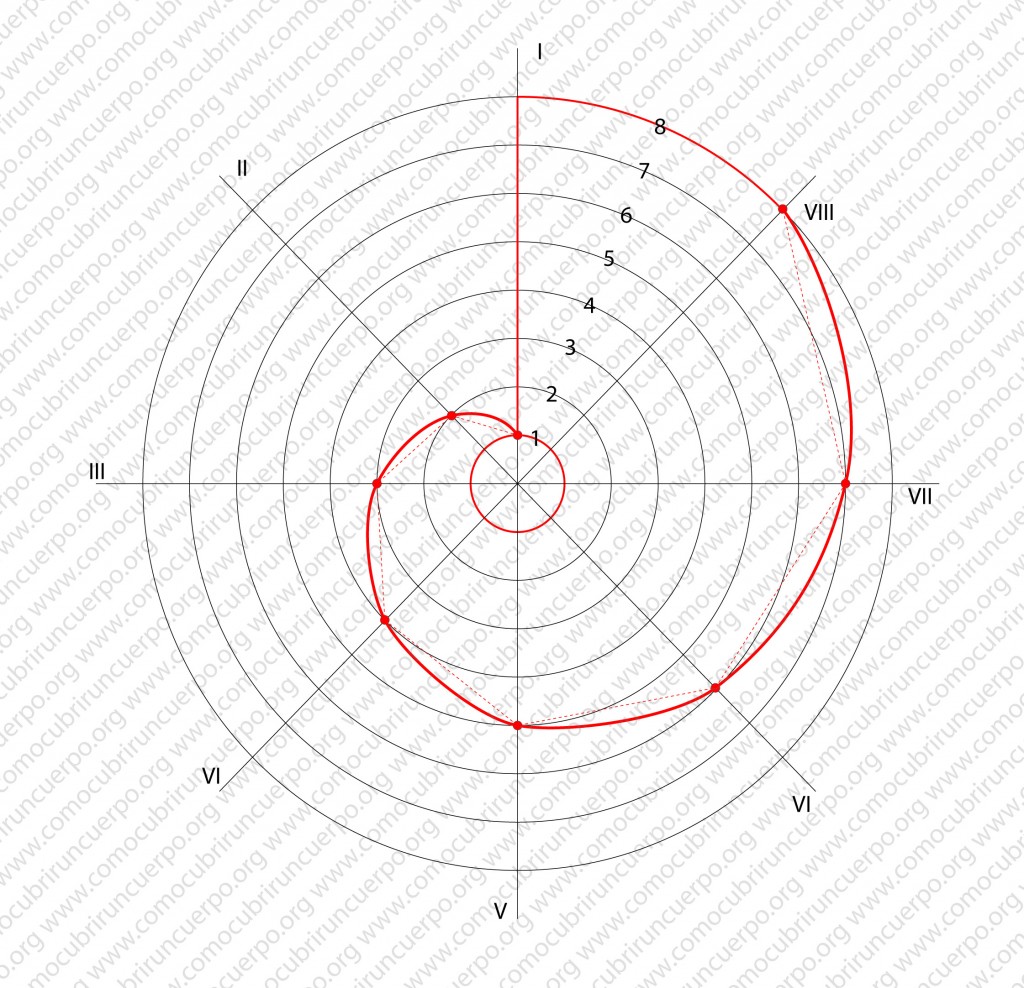
Con la ayuda de una línea de curvas trazaremos la espiral de Arquímedes.
Ya hemos obtenido nuestro volante de caracol mediante la espiral de Arquímedes.
Volante de caracol generado por círculos.
Ya hablamos de ellos en el post anteriores. Son círculos o sectores circulares cosidos entre sí.
En post sucesivos enseñaremos cómo combinar estos volantes de caracol generados por espirales y los generados por círculos.
Este post continúa en «Aspecto y montaje de los volantes de caracol«