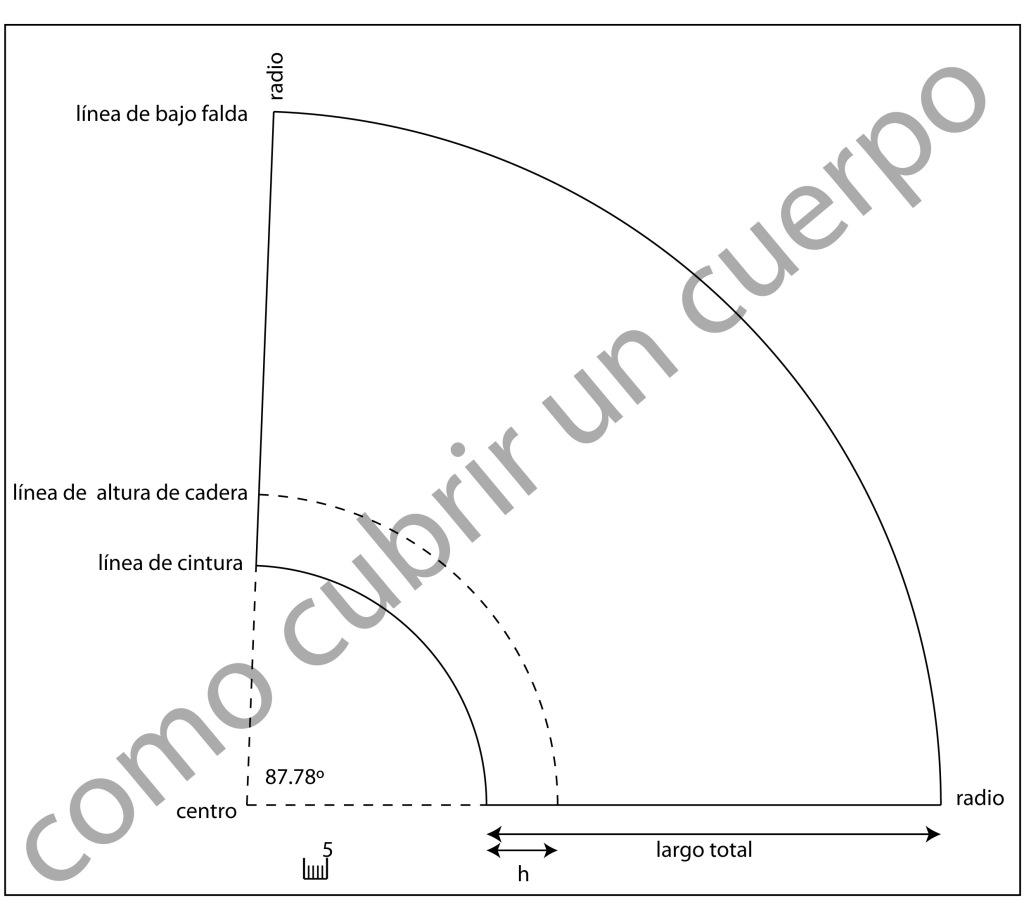
Patrón de la falda (5), Faldas circulares de menor vuelo.

El desarrollo plano de un cono recto tiene el siguiente aspecto.

α= grados del sector circular

r = el radio necesario para generar dicho sector circular

r’= el radio necesario para generar el perímetro de la base.

Para calcular los grados del sector circular (α) utilizaremos la siguiente fórmula:

α=(r’/r)*360

 

Si el perímetro de la base es la cintura de la falda, sabremos que el contorno completo de la cintura será igual a  2*π*r’, por lo que el perímetro de la medida de cintura, que en las tablas es la mitad del contorno entero será igual a π*r’ asi  c= π*r’ ,  r’= c/π

Por lo que:

α=((2c/π)/r)*360

siendo α los grados del sector circular, y c la cintura.

Si queremos cortar una falda de unos determinados grados, la única variable que nos faltará de la ecuación anterior será el valor r.

r= (c*360)/(π* α)

Con esta simple fórmula podremos calcular el sector circular hasta el largo deseado para cortar una fada con la medida de la cintura justa de cintura, en el caso en que la morfología del hombre fuera recta desde  la cintura hasta los pies ( caso de la Conformación Drop 0 o positiva, correspondientes a los obesos), en todos los otros casos por ahora sólo tenemos un sector circular que nos da un cono con la cintura justa.

Si queremos encontrar el mismo radio que incrementándolo de la altura de cadera nos dé un sector circular con los mismos grados y que la curva sea igual al perímetro de cadera, su fórmula será:

r+h=(k*360)/(π* α)

siendo h la altura de cadera  y k el medio perímetro de caderas, de ahí:

r=((k*360)/(π* α))-h

y juntando las dos ecuaciones:

 (c*360)/(π* α) =((k*360)/(π* α))-h

Despejando del valor α nos va a dar el valor mínimo del ángulo del sector circular para poder albergar el perímetro entero de cadera. Por lo que

 α =(360*(k-c))/π*h

Así por ejemplo una falda de la talla 44 de mujer estatura 160 que tiene de contorno de cintura 40, de contorno de cadera 52, de entrepierna 71,5 y de largo de pierna 99 la falda circular de mínimo vuelo será de:

α =(360*(52-40))/((π*(2*(99-75.5)/3))=87.78

En el caso de cortar la falda para un caballero de la talla 50 con un DROP – 5 (Conformación normal) que tiene la misma cadera, 52 de cintura tiene  45 y de montante 24.75 el valor de α es:

α =(360(52-45))/π*(2*24.75/3)= 48.62

Vemos que hay una gran diferencia entre el ángulo mínimo para cortar una falda capa para mujer u hombre, ello se debe a que la diferencia de cintura y cadera es mucho más pronunciada en la mujer que en el hombre.

Una vez tenemos el ángulo podemos proceder a cortar la capa trazando primero el radio de la falda, rotando este desde el centro para crear un ángulo igual a  α  y a partir de la intersección de estos dos radios que será el centro, trazaremos el radio de la cintura que lo calcularemos con la siguiente fórmula:

r=(c*360)/ (α.π)

Trazaremos el arco a partir del centro hasta los dos radios. A partir de la intersección del arco con el radio pondremos la medida del largo total de la falda y acabaremos trazando el bajo realizando otro arco desde el mismo centro,  si queremos comprobar la medida de la cadera, a partir de la intersección línea de cintura con el radio de la circunferencia aplicaremos la altura de caderas hacia el bajo, trazaremos otro arco que será la línea de caderas.

En la próxima ilustración exponemos la falda circular de menor vuelo realizada sobre las medidas más arriba expuestas de nuestras medidas de la talla 44(169)mujer.

Evidentemente en el caso de cortar una falda mayor al ángulo menor de cada talla no tendremos de preocuparnos del ancho de la cadera ya el vuelo siempre será mayor que la medida de la cadera.

Lo explicado para este blog sirve evidentemente para niño y niña cambiando únicamente las medidas.

Aconsejo consultar los post relativos a la cintura y a la cadera, en caso de que algo no se entienda, si tenéis dudas no dudad en preguntar.

Este post sigue en «Cálculo para el trazado de las faldas circulares de menor vuelo»