Concepto de gradación o escalado
El escalado o gradación es la técnica por la que podemos patronar directamente a partir de una talla dada otras tallas Sin necesidad de re-trazar uno a uno los patrones del al talla base.
Llamaremos talla base a la talla de la que haremos partir la gradación tanto en sentido positivo (tallas superiores) como en negativo (tallas inferiores).
Supongamos que tenemos una forma simple, por ejemplo un rectángulo, y una sucesión de números con un incremento proporcional y constante , por ejemplo 10. 20 30 .40 .50 60, 70, 80, y 90 y que determinamos que uno de los lados del rectángulo hace 5 cm siempre y el otro es una proporción de la lista de los números expuestos (las decenas correlativas)
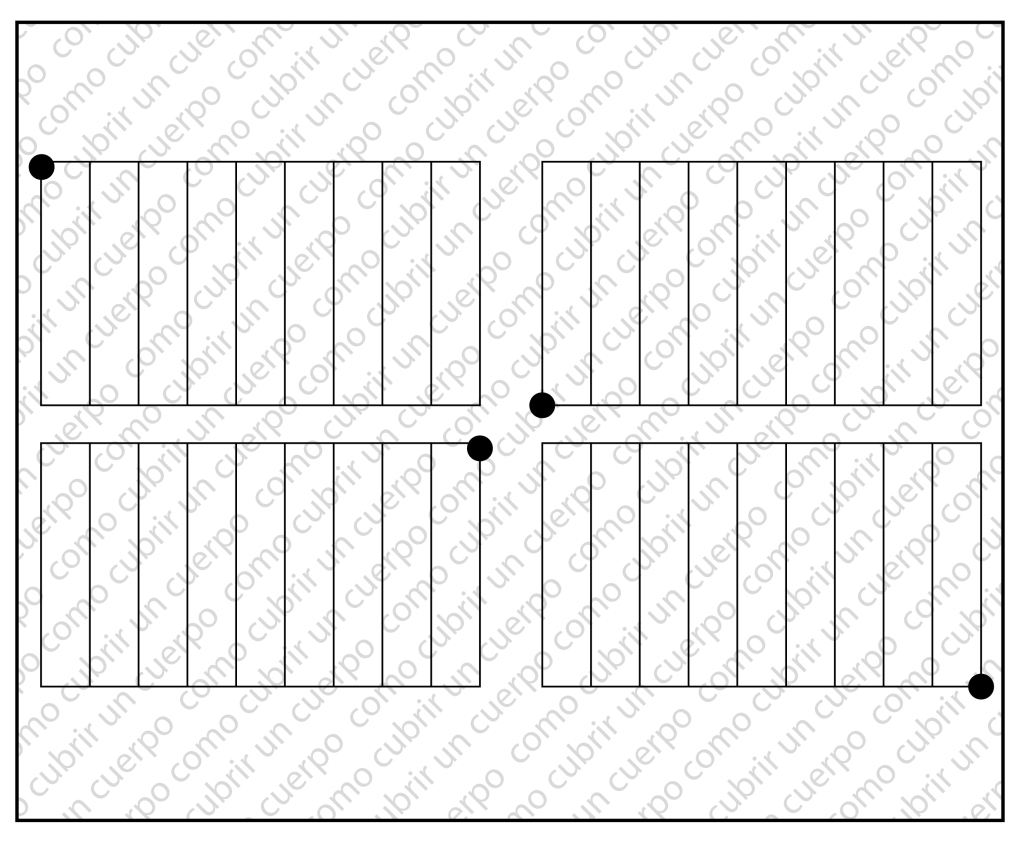
Si el lado proporcional es el del eje de las X ( horizontal al trazado ) y el fijo el eje de las y si el lado de los anchos(horizontal, eje de las X) tiene una proporción de un décimo (N/10, siendo N un número de la lista ) nos encontraremos con los siguientes rectángulos: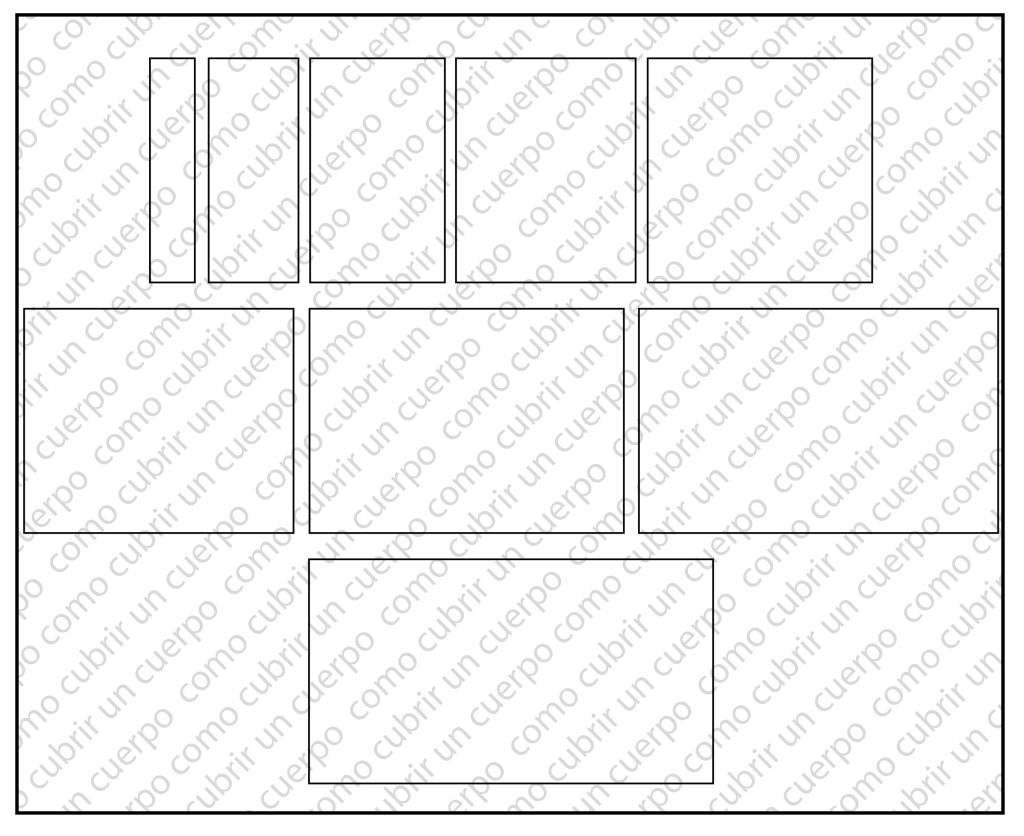
Si juntamos todos los rectángulos encontrados por el mismo punto de cada figura (punto de ancla o anclaje) obtendremos el siguiente diagrama.
La figura anterior sería una gradación o escalado horizontal ya que las coordenadas que varían son las del eje de las x, o sea de los anchos.
Vemos que el diagrama nuestra el dibujo de una escalera, una serie de peldaños consecutivos…. No fueron muy originales con el nombre, ¿verdad?
El nombre de gradación también es muy lógico ya que cada figura crece de grado en grado.
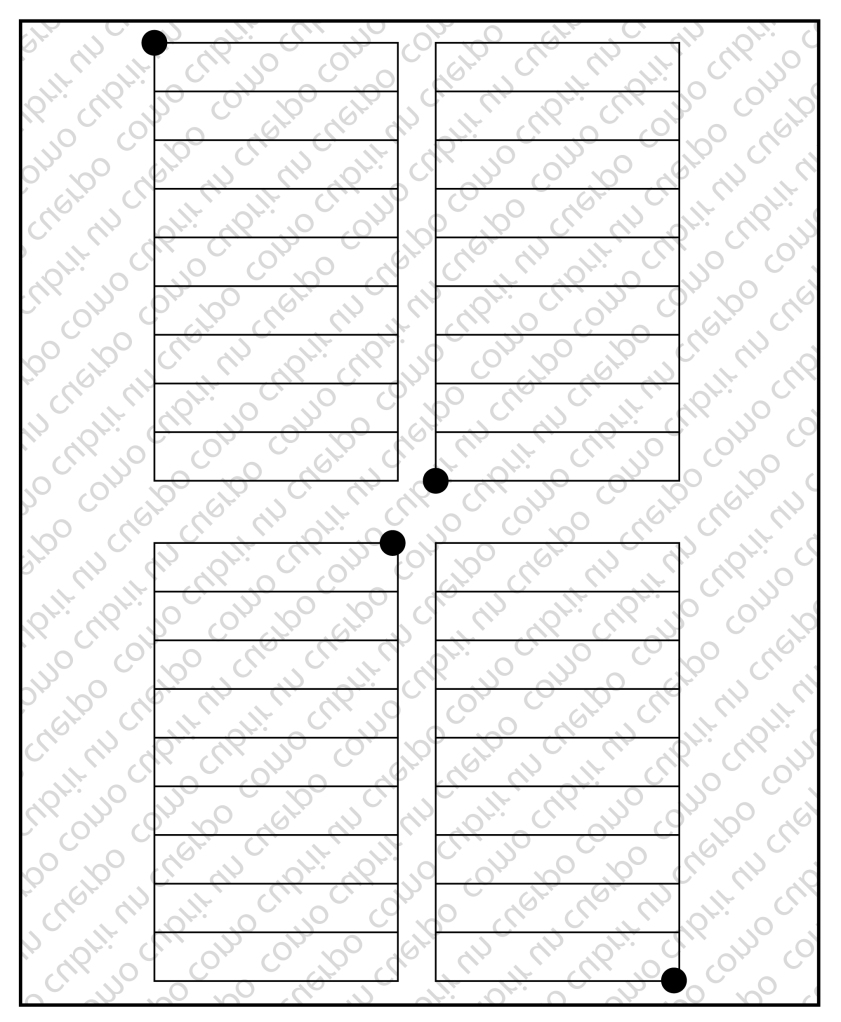
Si hiciéramos lo mismo cambiando el eje que es proporcional y el que es constante obtendríamos
Y si juntáramos todos los puntos por uno común obtendríamos:
En este caso al ser proporcional el eje de las Y y constante el de las X hablaríamos de una gradación escalados de largos
Si gradáramos los dos ejes nos encontraríamos juntando todos los elementos por los mismos puntos el siguiente diagrama y sería una Gradación de anchos y largos o una gradación o escalado mixto. Si uniéramos todos los puntos que unen sus homólogos encontraríamos lo que se llaman las líneas de entretallas, en este ejemplo dos coinciden con el eje de las y de las x respectivamente.
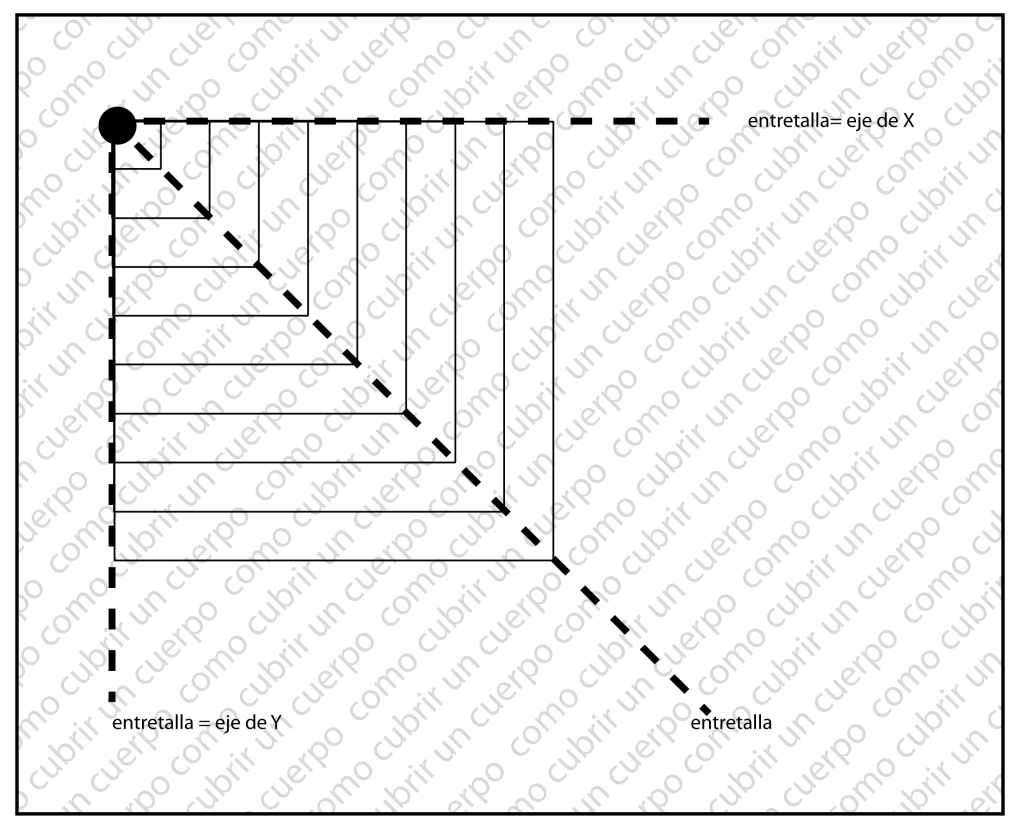
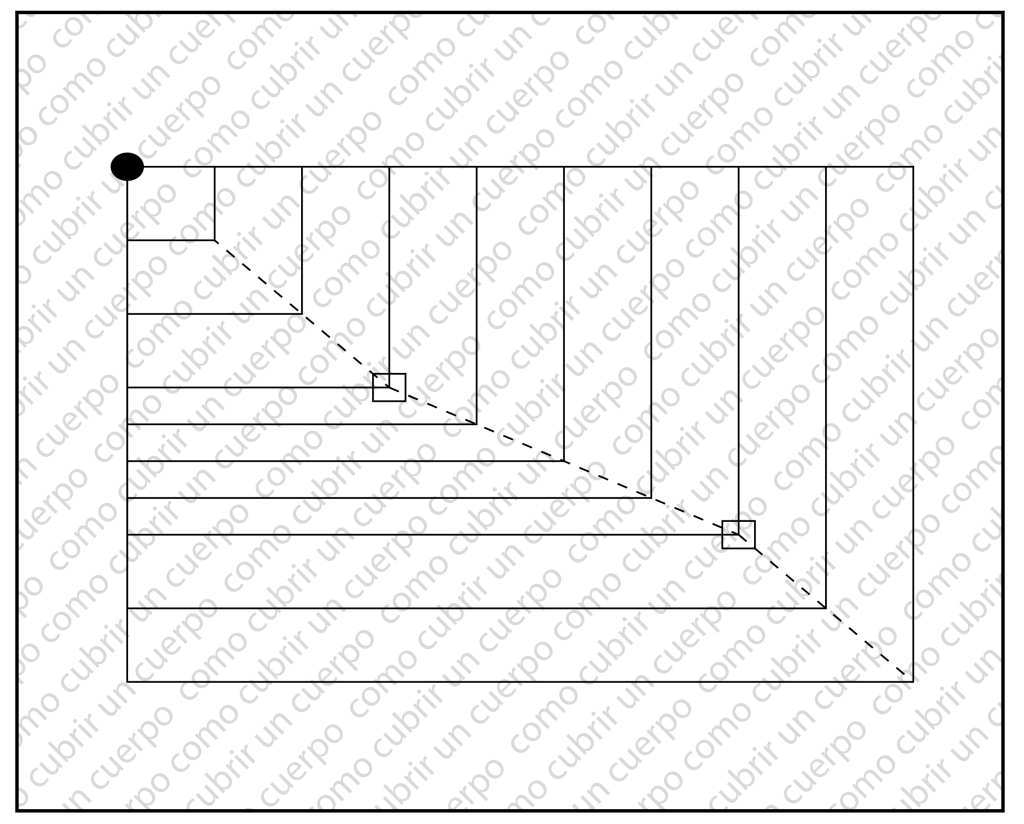
Si utilizáramos los números de incremento constante en el eje de las X, y en el eje de las Y utilizáramos otra serie por ejemplo: 10, 20, 30, 35, 40, 45, 50, 60 70 y en ambos ejes la proporción fuera de 1/0 nuestra plancha de gradación mixta del rectángulo presentaría el siguiente aspecto.
En la ilustración anterior vemos representado por un punto negro el punto de ancla, y por una línea discontinua la entretalla Ésta empieza con una inclinación y que a partir de un momento (he hemos señalado con cuadrados vacíos ), la inclinación cambia.
Ellos es debido a que una de las progresiones de los números a los que aplicamos la proporción de 1/10 deja de ser constante. Cada vez que una de las progresiones cambia el incremento entre el número anterior y posterior provoca un punto de quiebre.
El punto de quiebre determina la fin de una progresión constante y el inicio de una nueva progresión constante.
Como habréis supuesto el rectángulo es el patrón, y las números progresivos son las cotas de una determinada mediad dentro de una tabla.
Si aplicamos los conceptos dados a un patrón estaremos escalándolo.
Ahora ya sabemos el concepto del escalado o gradación, en el próximo post hablaremos de las ratios y a partir de allí ¡ya podréis escalar o gradar patrones!.
El escalado es una consecuencia lógica del patronaje: quien sabe patronar sabe escalar, sólo necesita las directrices necesarias para abrir los ojos.
Este post continúa en «Gradación 2: cómo hallar los ratios«