Gradación 2 Cómo hallar las ratios

Aconsejamos de haber leído el post relativo al patronaje de la falda recta y el post anterior Gradación (1). 

Llamaremos ratio (r) a la variación de incremento constante entre dos variables de la misma secuencia que nos dará una línea de entretalla constante y con una determinada inclinación,  sin puntos de quiebre.

Si en una entretalla encontramos uno o más puntos de quiebre, deberemos  calcular tantas ratios como puntos de quiebre tenga la entretalla.

La ratio, compuesta de dos valores, uno para el eje de las X y el, otro para el eje de la Y,  el valor de X e Y será lo que determinará la inclinación de la línea de entre talla entre des  puntos de quiebre.

Si disponemos de una tabla completa de cálculo como las que podemos encontrar de la falda en la categoría de tablas de medidas o consultando los post anteriores, podemos obtener las ratios restando la talla superior de la inferior mientras que la proporción se mantenga constante,  o sea que no haya un punto de quiebre

Si  no disponemos de la tabla competa de cálculos podemos deducir todas las ratios fácilmente utilizando sólo las proporciones de las variables.

Las fórmulas, por ejemplo en el post relativo al corte de la falda,  son unas proporciones (multiplicaciones y divisiones) y sumas o restas que se aplican a una serie de  variables (letras que representan los datos de las tablas antropométricas).

De cada una de las fórmulas sólo nos interesará la multiplicación y la división de la variable, no la del o la de los números ya que para todas las tallas nos dará un valor constante:

Así  +(K/2)+1 para lo que nos interesa será + K/2, o +P/4+3+8 será para nosotros +P/4 y +((2(P+1)/4)*3) seráv2 P/4 o lo que es lo mismo p/2

Si las variables son la secuencia de los números 4, 8, 12, 16

La  fórnula +(K/2)+ 1 tendrá la ratio rK/2, o sea la proporción que calcula de la variable (K/2), la calcularemos en la ratio de la secuencia. Vemos que los números de la secuencia crecen de 4 en 4 por lo que la ratio del punto será 4/2= 2

Para comprobarlo podemos calcular las fórmulas para cada uno de los números dados y su resultado restarlo con el inmediatamente inferior:

Si k es igual a 4: +(K+1)+1)  =  +(4/2)+1= 3.

Si k es igual a 8: +(K+1)+1)  =  +(8/2)+1= 5.

Si k es igual a 12: +(K+1)+1)  =  +(12/2)+1= 7.

Si k es igual a 16 +(K+1)+1)  =  +(16/2)+1= 9.

Como podemos comprobar los resultados se incrementan por 2 unidades como habíamos calculado anteriormente.

Cuando en un patrón decidimos poner el valor de la tabla entero, sin proporción por ejemplo largo total (LG), en verdad estamos poniendo una variable, ya que la fórmula puede ser +1(LT), o sea que la variable la estamos multiplicando por 1

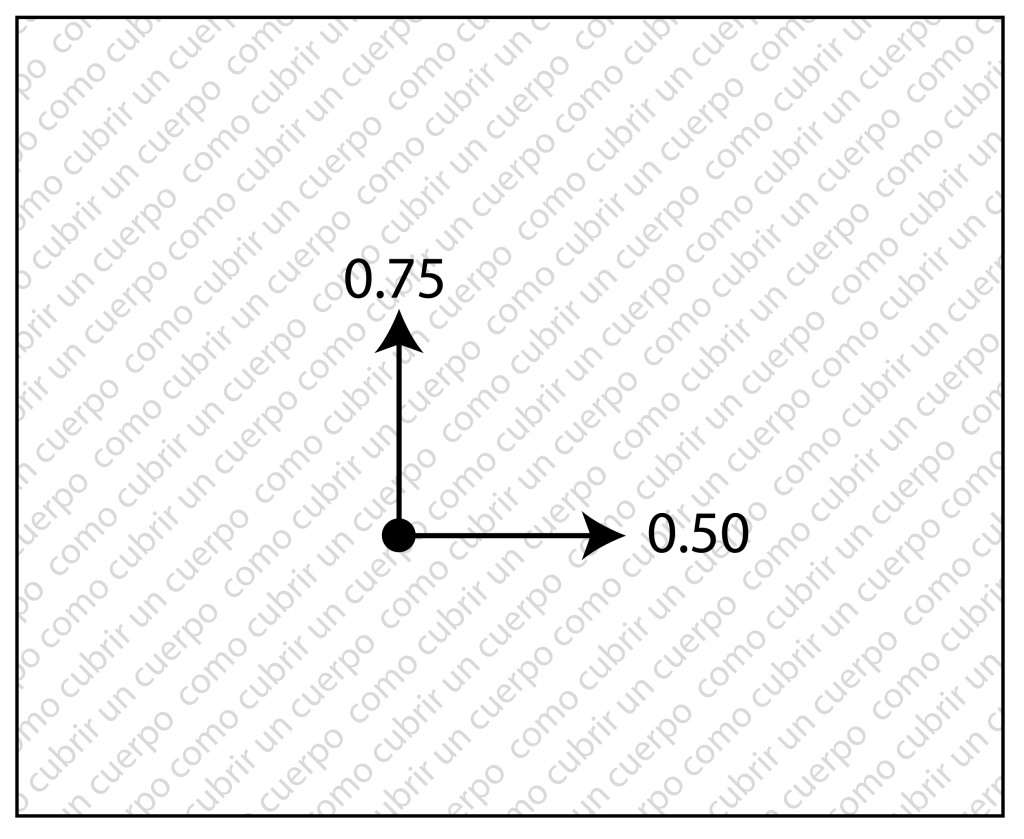
Las ratios se representan con dos flechas como en la ilustración que sigue:

Debemos leer la ratio de la siguiente manera, para cada talla superior encontraremos un incremento de 0.75 cm del punto en el eje de la Y lacia la dirección de la flecha y de 0,50 en el eje de las X, para cada talla inferior encontraremos los mismos valores pero con las direcciones opuestas de las tallas que aparecen en la ilustración.

Pondremos en práctica todos estos conceptos en el próximo post: La gradación de la falda.

Aunque parezca confuso en el próximo post veréis que es ¡un juego de niños!.

Este post continúa en «Gradación 3: Teorema de Tales de Mileto para dividir las entretallas»

 Cargando ...