Aspecto y montaje de los volantes de caracol
En este post vamos a hablar de cómo se montan los caracoles y cómo calcularlos.
Este artículo es la continuación del post: El volante o volado de caracol que fue publicado en este blog el 7 de enero de 2014, que podéis encontrar en el índice superior de este blog o en la rúbrica «índice y escuela o bien clicando sobre el enlace de su nombre.
Los dibujos de este post no están hechos a caso, los volados o sea la parte que desarrolla el volante como la parte de funge de costura están dibujados proporcionalmente, por lo que el frunce que mostramos en las ilustraciones de este post son correctas. El frunce lo hemos dibujado de forma de hacerlo comprensible aún en detrimento de su representación artística: en el caso en que un volante o parte de éste esté muy fruncido se “desparrama “o abre en todas las direcciones (hacia la derecha, hacia la izquierda hacia delante y hacia atrás) en nuestro caso los hemos dibujado como si quedaran “tiesos” y con una onda similar para evidenciar la fuerza del frunce de cada volado y de cada parte del volado de los volantes que expondremos a continuación.
Por otra parte la apariencia del volante cambia muchísimo según la tela que utilicemos: su nervio, apresto o en el caso contrario caída o livianidad darán a nuestro volante un aspecto concreto. Dos telas diferentes montadas con un mismo volante darán resultados totalmente diferentes.
Aspecto y montaje de los volantes de caracol: El caracol de clavel.
Vamos a empezar por las circunferencias o caracol de clavel.
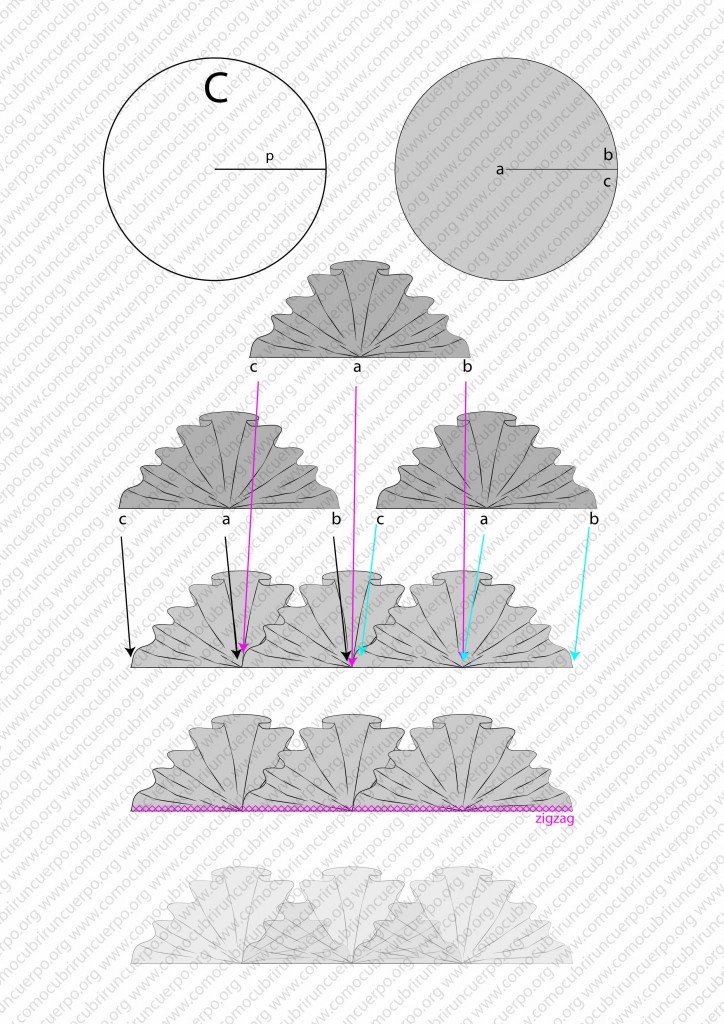
Las vamos a llamar “C” en nuestros esquemas. El diámetro de la circunferencia será el paso (p) o si preferimos el ancho del volante.
Cada dos circunferencias aumenta nuestro volante de “p “, contando siempre “2p” para la primera circunferencia, así podemos establecer la fórmula:
Largo del volante = (número de circunferencias * p)+ p.
Este tipo de volante se cose con un zigzag que une los círculos, se utiliza generalmente con telas muy livianas y transparentes, como puede ser organza o tul.
En la siguiente ilustración enseñamos la forma de montarla y hemos dibujado en la parte inferior que apariencia da en una costura recta.
Aspecto y montaje de los volantes de caracol: Volante de caracol con sectores circulares
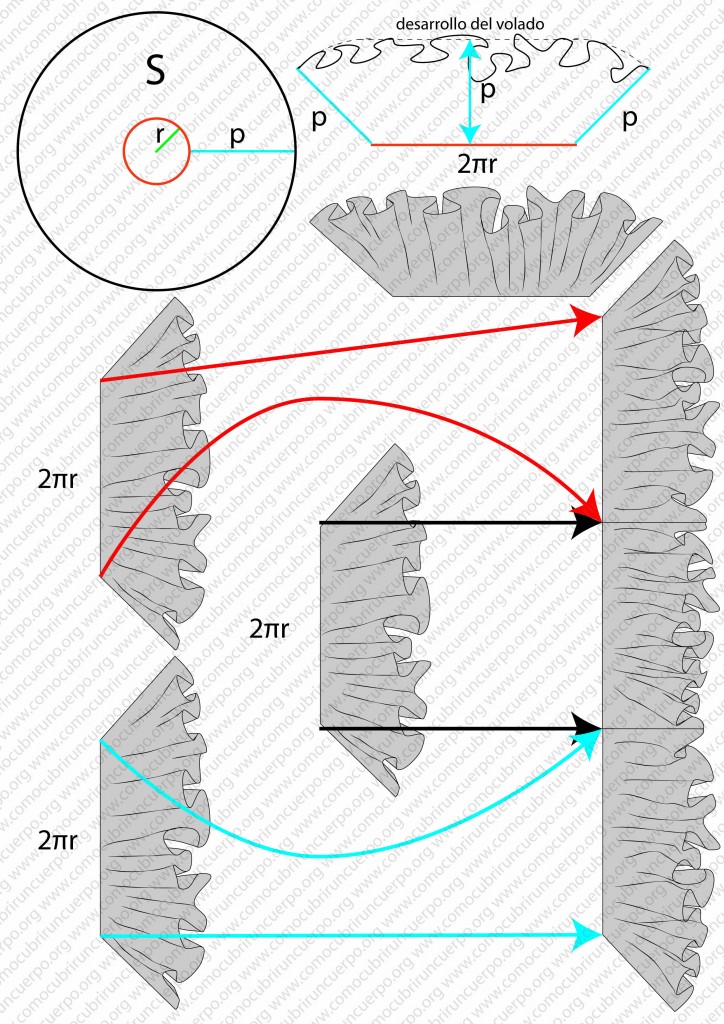
EL volante de caracol cortado con sectores circulares tiene la peculiaridad que el desarrollo de la volada es siempre constante, así como el ancho del volante o paso (p).
Les llamaremos “S”.
Para calcular el desarrollo del volante deberemos aplicar la fórmula 2πr, el ancho del volante será “P”. El volado o desarrollo del volante será 2π(p+r).
En el dibujo que sigue hemos plasmado la el desarrollo del volado alineando el perímetro de la circunferencia interior y dibujando el desarrollo del volado encima del perímetro interior o costura. .
Aspecto y montaje de los volantes de caracol: Volante de caracol trazado a partir de la espiral de Arquímedes.
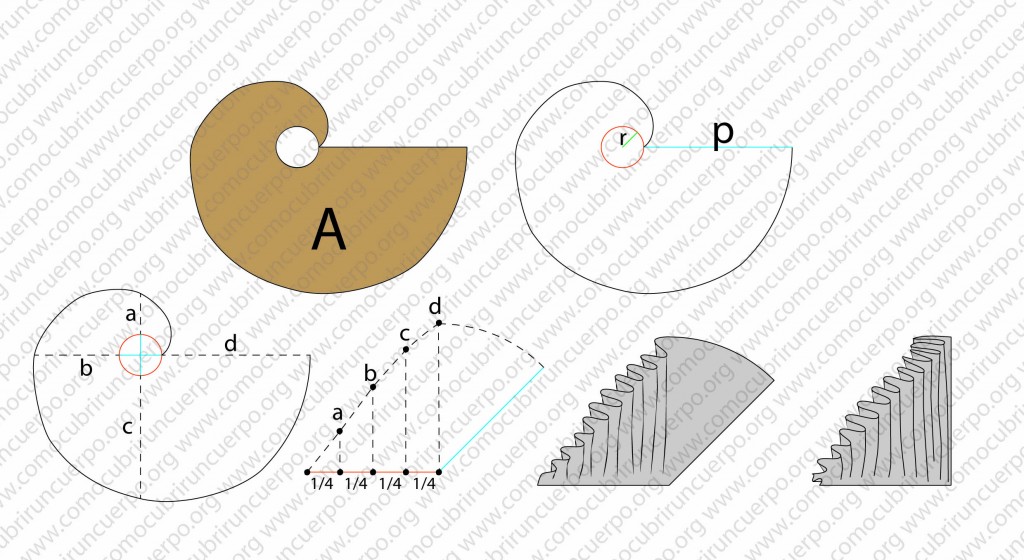
En la siguiente ilustración hemos realizado el trazado del volante que genera una espiral de Arquimedes en cuyo centro hemos ahuecado una circunferencia,.
El valor del perímetro de la circunferencia interior es igual a 2πr.
Prolongando el ancho final del volante de la espiral hemos hallado una diagonal que corta la circunferencia interior (la que será el largo de la costura en dos).
Hemos prolongado esta línea en la misma dirección hasta que ha vuelto a cortar la espiral de Arquímedes.
Luego, desde el centro del círculo anterior hemos trazado un diámetro que corta perpendicularmente al diámetro ya trazado. Y hemos prolongado sus extremos hasta que se corte con las líneas exteriores de la espiral.
Estos dos diámetros cortan la circunferencia interior en cuatro partes mediante cuatro líneas perpendiculares entre ellas : dividirán el perímetro de la circunferencia interior o la costura en cuatro partes iguales.
Las prolongaciones de estos diámetros nos generan unas líneas de cota que nos darán el desarrollo del volado en cada uno de los cuartos. (segmentos: a,b,c y d)
Hemos representado el perímetro del círculo interior mediante la línea recta de color rojo que hemos cortado con cuatro perpendiculares, estas perpendiculares las hemos acotado con la distancia hallada encima del área de nuestro volante, segmentos: a, b, c, y d. Por último hemos juntado estos puntos para representar el crecimiento del volante a medida que avanzamos en la costura hasta su apogeo (línea d) en que encuentra todo su desarrollo.
En la última ilustración hemos recogido el volado para dejarlo a escuadra con la línea del perímetro que representa la costura.
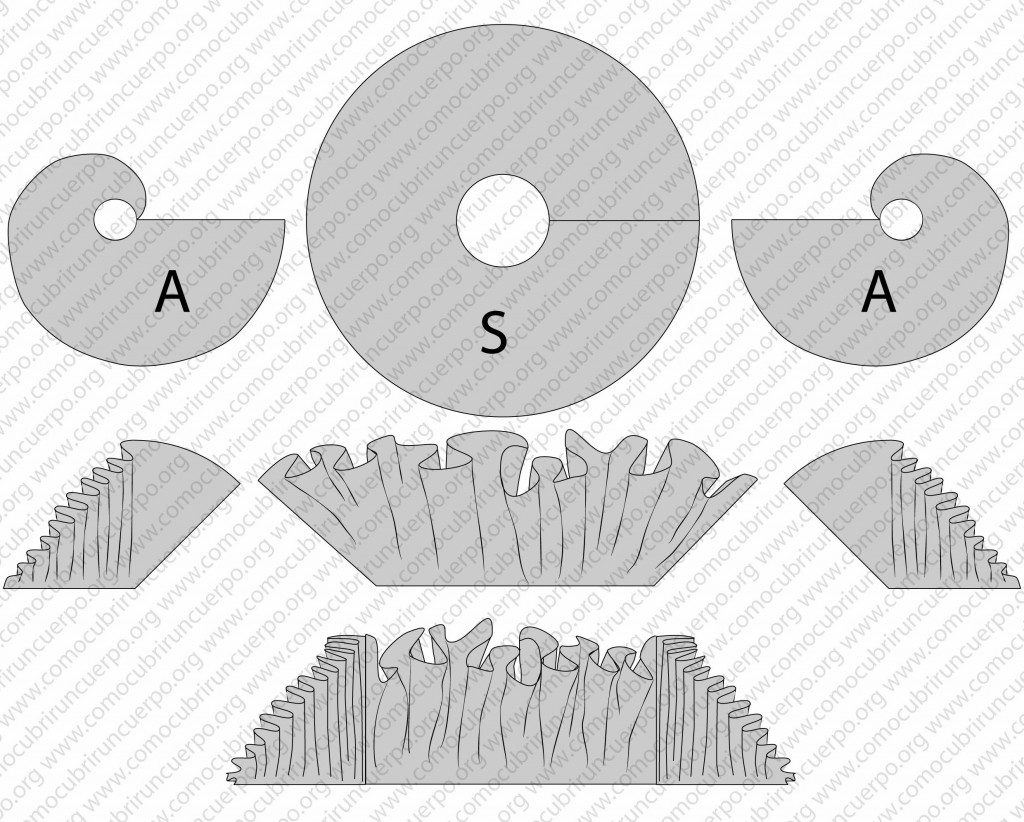
En esta próxima imagen enseñamos como podemos montar varias espirales entre sí. En este caso hemos montado dos volantes generados por espirales de Arquímedes y un volante generado por un sector: estructura A+S+A
Vemos como los frunces de los volantes A y S son diferentes.
Aspecto y montaje de los volantes de caracol: Volantes generados con un segmento (P/2), o con formas geométricas (P/3, P/4, …)
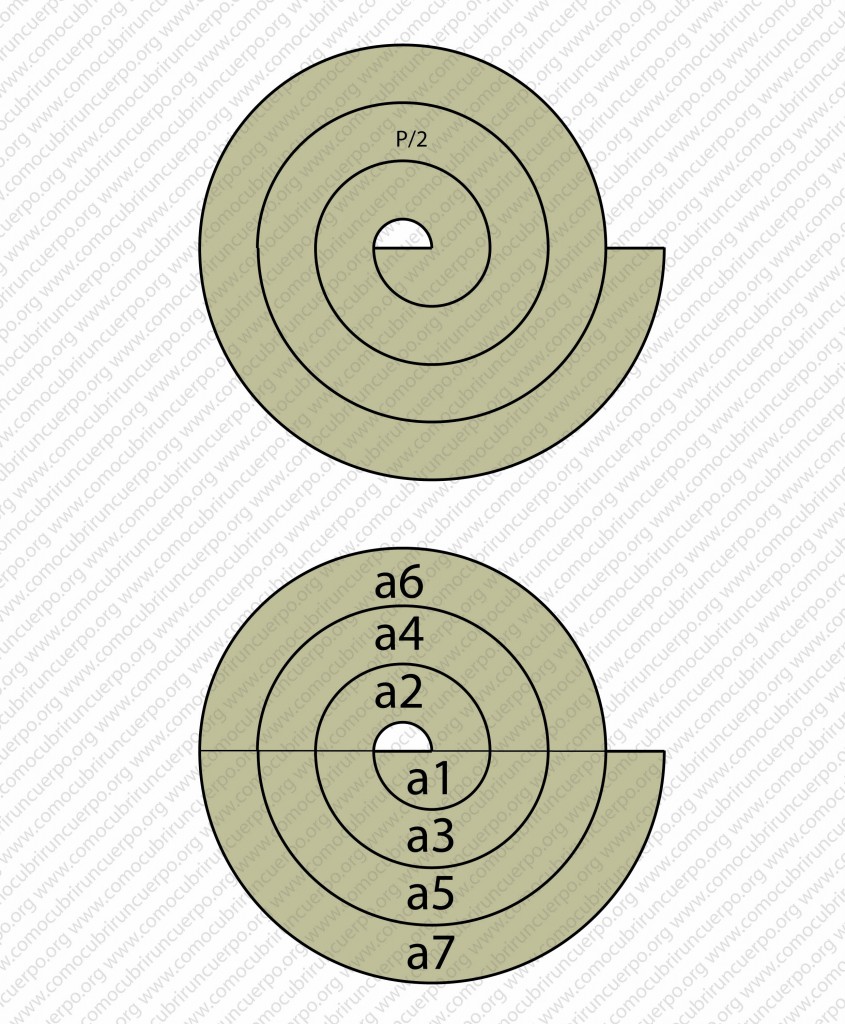
En la siguiente ilustración hemos reproducido en su parte superior el trazado que mostramos en su día del trazado del volante de espiral P/2, recordemos que en este tipo de espirales el paso (ancho de volante) es constante desde el inicio hasta su fin y está generado por un segmento (dos centros).
En la imagen inferior de la ilustración siguiente hemos dividido la espiral en dos parte iguales (pasando por los dos centros). De esta forma hemos dividido la espiral en varios sectores circulares regulares: a1, a2, a3, a4, a5, y a6.
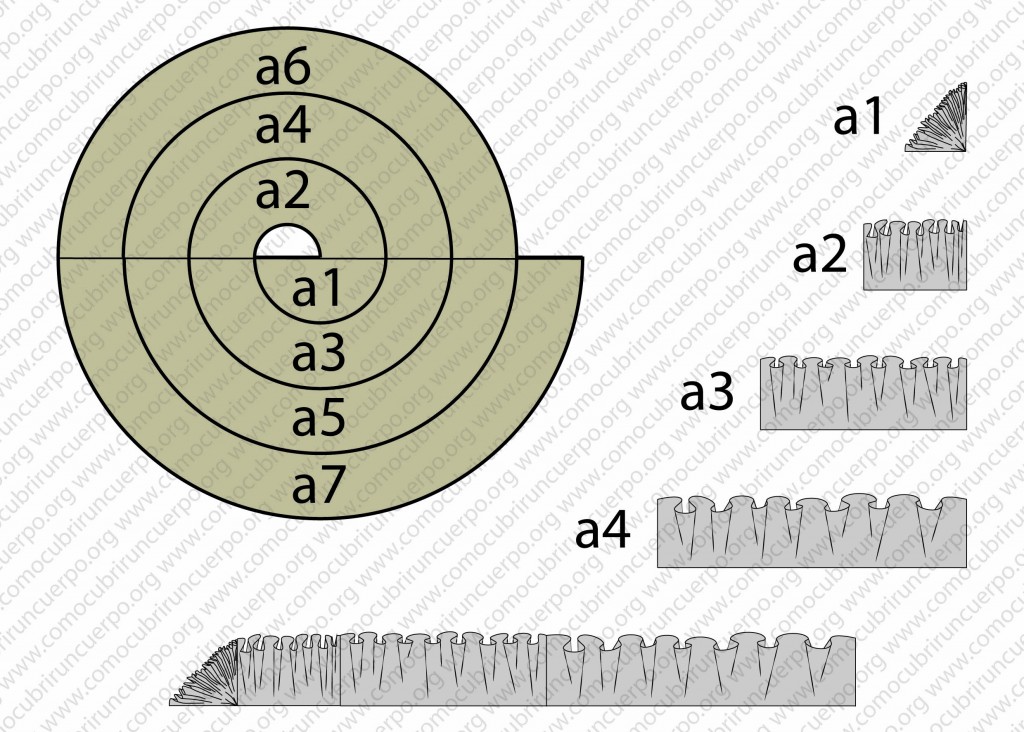
En la imagen sucesiva veremos cómo hemos trazado las imágenes pertenecientes a cada uno de los sectores calculando el largo de costura y el largo del volado generado por el sector.
Vemos que cada sector superior desarrolla un volado menor y así será cada vez que el volante se identifique con sectores que se aparten más del centro de la espiral.
La última imagen de la siguiente ilustración muestra el volante desde el sector a1 hasta el sector a4.
Si comparamos el frunce vemos que cada vez es menos intenso.
De cómo calcular los frunces y por lo tanto de cómo calcular la pérdida de frunce en un volante P/2 hablaremos en otro post.
Siguiendo el mismo procedimiento podéis realizar vosotros mismos las imágenes de los volantes generados por espirales P/3, P/4 etc.